Understanding Exponential Smoothing Factor: Definition and Application

Understanding the Exponential Smoothing Factor

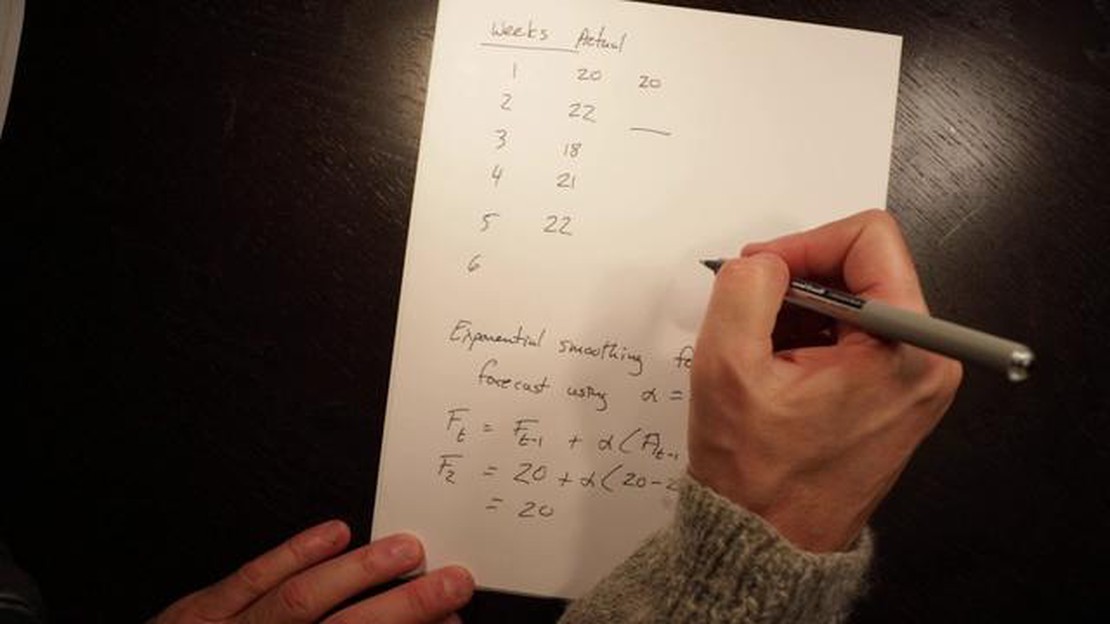
Exponential smoothing is a popular statistical method used to forecast data, particularly time series data. It is based on the idea that recent observations have more influence on future predictions than older ones. The exponential smoothing factor is a crucial parameter in this method that determines the weight given to different observations.

Table Of Contents

The exponential smoothing factor, also known as the smoothing constant or alpha, is a value between 0 and 1. Larger values of alpha assign more weight to recent observations, resulting in a more responsive forecast. Conversely, smaller values of alpha give more weight to older observations, leading to a smoother forecast.

The choice of the exponential smoothing factor depends on the characteristics of the data being analyzed. If the data is highly variable and subject to fluctuations, a smaller value of alpha may be preferred to reduce the impact of outliers. On the other hand, if the data is stable and trending, a larger value of alpha may be more appropriate to capture recent changes.

Understanding the exponential smoothing factor is essential for accurate forecasting. It allows analysts to strike a balance between responsiveness and stability in their predictions and adapt the method to different data patterns. By selecting the optimal value for alpha, analysts can improve the accuracy of their forecasts and make more informed decisions based on the insights gained from the data.

Exploring Exponential Smoothing Factor

Exponential smoothing factor, also known as the smoothing coefficient or alpha (α), is a parameter used in exponential smoothing models to control the weightage given to the past observations while forecasting future values. It determines the rate at which the influence of past observations exponentially decreases as newer observations are included in the calculation.

The exponential smoothing factor can take values between 0 and 1, where 0 represents no weightage to past observations and 1 represents full weightage to past observations. The choice of the value depends on the characteristics of the time series being analyzed and the desired level of smoothing.

When the exponential smoothing factor is set closer to 1, the forecast will be more sensitive to recent observations, resulting in a model that quickly adapts to changes in the time series. This is suitable for time series data that exhibit high volatility or sudden changes. However, if the data is noisy or contains outliers, a higher smoothing factor may lead to overfitting and inaccurate forecasts.

On the other hand, setting the exponential smoothing factor closer to 0 gives more weightage to past observations and smooths out any short-term fluctuations or noise in the data. This is useful when dealing with time series data that has low volatility and a stable trend. However, a smaller smoothing factor may result in a slower response to changes in the time series and may miss capturing sudden shifts or patterns.

To determine the optimal value for the exponential smoothing factor, various techniques such as grid search, cross-validation, or optimization algorithms can be employed. Additionally, domain knowledge and understanding the underlying data patterns can help in selecting a suitable value for the smoothing factor.

It is important to note that while the exponential smoothing factor plays a crucial role in determining the accuracy and responsiveness of the forecasting model, it is not the sole parameter to consider. Other factors such as trend, seasonality, and level components should also be incorporated in the model to ensure better forecast accuracy.

Factor Value	Forecast Responsiveness	Smoothing Level
0	Low	More weightage to past observations, less responsive to changes
1	High	More responsive to changes, less weightage to past observations
0.5	Medium	Moderate weightage to past and recent observations

Read Also: Learn how to successfully trade in Nifty options

Importance of Exponential Smoothing Factor

Exponential Smoothing Factor (ESF) plays a crucial role in various fields such as finance, economics, and supply chain management. It is a parameter used in the exponential smoothing method, which is a popular technique for forecasting future values based on past data.

Accuracy: The choice of an appropriate ESF is essential to achieve accurate forecasts. The ESF determines the weight given to recent observations compared to older observations. A higher ESF assigns more significance to recent data points, resulting in a more responsive forecast that quickly reflects any fluctuations or changes. Conversely, a lower ESF gives more weight to older data points, which can provide a smoother forecast that is less sensitive to short-term variations.

Read Also: Is trading on iPad worth it? Advantages and disadvantages of mobile trading

Adaptability: The ESF allows the forecast to adapt to changing patterns and trends in the data. By adjusting the ESF, the forecast can emphasize recent changes or disregard older patterns. This adaptability is crucial in industries where demand or market conditions can rapidly change, such as retail, fashion, or technology.

Efficiency: Exponential smoothing with an appropriate ESF can provide efficient forecasts with minimal computation. The method avoids the need for complex calculations or the use of extensive historical data, making it suitable for applications where real-time or near real-time forecasting is required.

Flexibility: The ESF can be adjusted based on the characteristics of the data being forecasted. For example, if the data exhibits high volatility, a higher ESF can capture the rapid changes more effectively. On the other hand, if the data is relatively stable, a lower ESF may be more appropriate to avoid overreacting to short-term fluctuations.

Forecast Evaluation: The ESF also plays a role in evaluating the accuracy of forecasts. By comparing the forecasted values with the actual values, analysts can assess the performance of different ESF values and fine-tune them for better predictions. This evaluation process helps to validate the forecasting model and improve its reliability over time.

In conclusion, the choice of the exponential smoothing factor is vital for accurate, adaptable, efficient, and flexible forecasting. Including the ESF in the process allows for dynamic adjustments to changing patterns and can provide valuable insights into the effectiveness of the forecasting model.

FAQ:

What is exponential smoothing factor?

Exponential smoothing factor is a parameter used in exponential smoothing models, which determines the weight assigned to the most recent observation when calculating the forecasted value. It represents how quickly the importance of past observations diminishes as new observations are incorporated into the forecast.

How is the exponential smoothing factor calculated?

The exponential smoothing factor is typically calculated using a smoothing factor alpha, which is a number between 0 and 1. The formula for calculating the exponential smoothing factor is: exponential smoothing factor = 1 - alpha.

What is the significance of the exponential smoothing factor in forecasting?

The exponential smoothing factor plays a crucial role in forecasting by determining the weight given to recent observations. A higher exponential smoothing factor gives more importance to recent observations, resulting in a forecast that is more responsive to recent changes in the data. On the other hand, a lower exponential smoothing factor gives more weight to past observations, resulting in a forecast that is more resistant to short-term fluctuations.

How does the choice of exponential smoothing factor affect forecasting accuracy?

The choice of exponential smoothing factor can have a significant impact on forecasting accuracy. A higher exponential smoothing factor provides more weight to recent observations, which can be beneficial when there are rapid changes in the data. However, this may also lead to overreacting to short-term fluctuations and may not capture long-term trends. Conversely, a lower exponential smoothing factor gives more weight to past observations, which can help in capturing long-term trends but may result in a less responsive forecast.

Are there any guidelines or best practices for selecting the exponential smoothing factor?

There are no strict guidelines for selecting the exponential smoothing factor, as it depends on the nature of the data and the forecasting objectives. However, some best practices suggest starting with a value of 0.1 for a moderately responsive forecast, and adjusting it based on the specific characteristics of the data and the desired forecast accuracy. It is important to consider the trade-off between responsiveness and stability when selecting the exponential smoothing factor.