How to manually calculate exponential: step-by-step guide

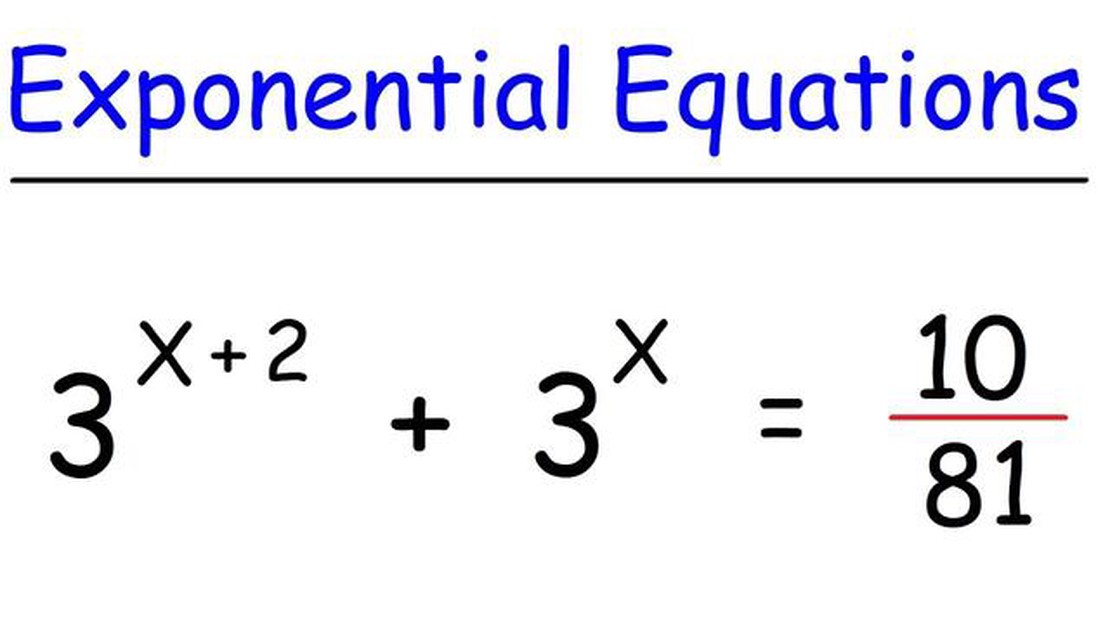
post-thumb

Calculating Exponential Manually: A Step-by-Step Guide

Calculating exponential functions is a fundamental concept in mathematics. Exponential functions are widely used in various fields, such as finance, economics, and science. Understanding how to manually calculate exponential values is essential for solving complex equations and modeling real-world phenomena.

Table Of Contents

In this step-by-step guide, we will explore the process of manually calculating exponential functions. We will discuss the basic principles and formulas involved, providing clear examples and explanations to help you grasp the concept and apply it in your own calculations.

Exponential functions consist of a base raised to an exponent, where the base is a constant and the exponent represents the power to which the base is raised. The result of an exponential function is a value that grows or decays at an increasing rate.

To calculate an exponential function manually, you need to understand the relationship between the base and exponent, as well as the properties of exponential functions.

By following this step-by-step guide, you will gain the knowledge and skills necessary to manually calculate exponential functions with confidence, enabling you to solve complex equations and make accurate predictions in various disciplines. So, let’s dive in and explore the fascinating world of exponential calculations!

How to calculate exponential: step-by-step guide

An exponential function is a mathematical function in which the exponent is a variable. It is commonly expressed in the form of y = a * b^x, where a and b are constants.

To manually calculate the exponential, follow these steps:

  1. Identify the base (b) and exponent (x) values: In the exponential function, the base value (b) is the number that is raised to a power, and the exponent value (x) represents the power to which the base is raised.
  2. Substitute the values of b and x into the exponential function: Replace the variables b and x in the exponential function equation (y = a * b^x) with their corresponding values to get the equation in terms of numbers.
  3. Solve the equation: Calculate the value of the exponential function using basic arithmetic operations (multiplication and exponentiation).
  4. Interpret the result: Once you have calculated the value of the exponential function, analyze the result in the context of the problem or situation being studied.

It is important to note that exponential functions can represent various real-world phenomena, such as population growth, compound interest, or radioactive decay. Understanding how to manually calculate exponential functions can help you gain insight into the behavior of these phenomena and make predictions based on the given data.

Understanding the concept of exponential

Exponential is a mathematical term that describes the growth or decay of a quantity at a constant rate. It is a fundamental concept in many fields, including mathematics, physics, finance, and biology.

In mathematics, exponential functions are functions of the form f(x) = a * bx, where a and b are constants and x is the variable. The constant a is called the initial value or the y-intercept, while the constant b is called the base or the growth factor.

Exponential functions have several important properties. First, they exhibit exponential growth or decay, depending on whether b is greater or less than 1. If b is greater than 1, the function will increase rapidly as x increases, demonstrating exponential growth. On the other hand, if b is between 0 and 1, the function will decrease rapidly as x increases, showing exponential decay.

Second, exponential functions have a constant ratio between any two consecutive values of x. This ratio is equal to the base b. For example, if the ratio between f(x) and f(x+1) is 3, then the base b is 3.

Third, exponential functions have a horizontal asymptote at y = 0 when the base b is less than 1. This means that as x approaches positive or negative infinity, the function will approach 0. However, if the base b is greater than 1, the function will not have an asymptote at y = 0.

Read Also: Learn How to Add a World Clock to Your Desktop on Windows 7

Exponential functions are used to model various natural phenomena, such as population growth, radioactive decay, and compound interest. They are also widely used in calculus and differential equations to solve various problems and analyze complex systems.

Understanding the concept of exponential is crucial in many fields, as it allows for the analysis and prediction of growth or decay patterns. By understanding the properties and behavior of exponential functions, we can make informed decisions, solve problems, and gain valuable insights into the natural world and the workings of the universe.

Identifying the base and exponent values

When manually calculating an exponential, it is important to identify the base and exponent values correctly. The base value represents the number that is being multiplied by itself, while the exponent value indicates how many times the base is being multiplied.

For example, in the exponential expression 23, the base value is 2, and the exponent value is 3. This means that the base value 2 is being multiplied by itself three times.

In some cases, the base value may be a variable or a complicated expression, making it important to correctly identify it before proceeding with the calculations. Once the base value is identified, the exponent value can be determined easily as it is usually written adjacent to the base value and indicated by the superscript.

By correctly identifying the base and exponent values, you can accurately calculate the exponential expression step by step.

Read Also: Understanding the Kelly's Formula and its Role in Financial Decision Making
Example:Calculate the value of 52
Solution:The base value is 5 and the exponent value is 2. This means that 5 is being multiplied by itself 2 times.
52 = 5 * 5
52 = 25

In this example, the base value is 5 and the exponent value is 2. By multiplying the base value 5 by itself 2 times, we get the result of 25.

Performing multiplication repeatedly

To manually calculate an exponential, you need to repeatedly perform multiplication. This involves multiplying a base number by itself a certain number of times, based on the exponent.

For example, if you have a base number of 2 and an exponent of 3, you would need to multiply 2 by itself 3 times. The calculation would look like this:

2 * 2 * 2 = 8

As another example, if you have a base number of 5 and an exponent of 4, you would need to multiply 5 by itself 4 times. The calculation would look like this:

5 * 5 * 5 * 5 = 625

By performing multiplication repeatedly, you can manually calculate the value of an exponential. This method can be useful when you don’t have access to a calculator or when you want to understand the underlying process of exponential calculations.

FAQ:

What is an exponential function?

An exponential function is a mathematical function in which the variable appears as an exponent.

Why would I need to manually calculate an exponential?

There are various reasons why you may need to manually calculate an exponential. It could be for educational purposes, to better understand how exponential calculations work, or to solve a specific problem that requires the use of exponential functions.

Are there any shortcuts or formulas to make manual exponential calculations easier?

Yes, there are certain shortcuts and formulas that can make manual exponential calculations easier. One example is the rule of exponents which states that when multiplying two exponential numbers with the same base, you can add the exponents. Another example is the power of a product rule which states that when raising a product to an exponent, you can distribute the exponent to each factor. These shortcuts can simplify the calculations and save time.

What is an exponential function?

An exponential function is a mathematical function in which the variable appears in the exponent.

See Also:

    You May Also Like