Understanding the Variance of EWMA: Exploring its Importance and Implications

Understanding the Variance of EWMA

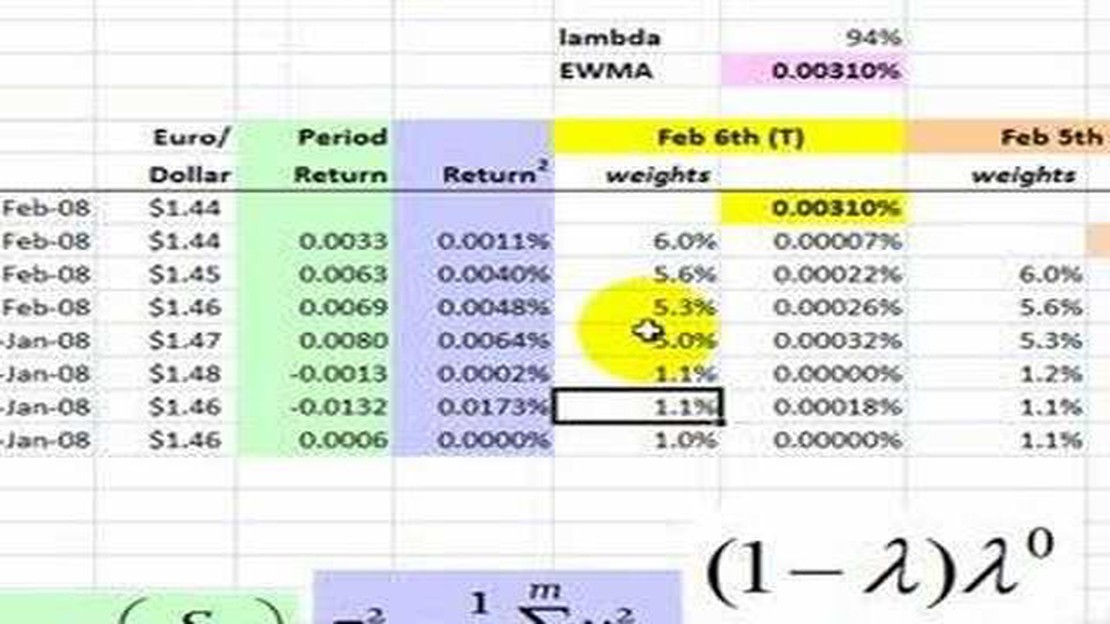
The Exponentially Weighted Moving Average (EWMA) is a statistical method widely used in finance and risk management for forecasting and analyzing time series data. It is particularly useful in situations where the underlying data is non-stationary or exhibits changing patterns over time. One crucial aspect of the EWMA is its variance, which plays a significant role in assessing the accuracy and reliability of the forecasted values.

Variance, as a measure of dispersion, quantifies the spread of the data points around the mean. In the context of the EWMA, it reflects the uncertainty or volatility associated with the forecasted values. By understanding the variance of the EWMA, analysts and decision-makers can gauge the level of confidence they can place in the forecasted results. A lower variance indicates a narrower range of potential outcomes, while a higher variance implies a wider dispersion of possible values.

Table Of Contents

The importance of understanding the variance of the EWMA lies in its implications for risk management and decision-making. A smaller variance suggests a more stable and predictable environment, reducing the potential for unexpected outcomes or losses. Conversely, a larger variance points to a more uncertain or volatile environment, calling for a more cautious approach and contingency planning.

Exploring the variance of the EWMA involves examining factors such as the smoothing factor (lambda), the length of the weighting window, and the characteristics of the underlying data. By conducting sensitivity analyses and scenario testing, analysts can gain insights into how different inputs and assumptions affect the variance and, consequently, the reliability of the forecasted results. This knowledge empowers decision-makers to make more informed choices and develop robust risk mitigation strategies.

In summary, understanding the variance of the EWMA is crucial for accurately assessing the uncertainty and volatility associated with forecasted values. By exploring the factors influencing the variance and conducting sensitivity analyses, decision-makers can make more informed decisions and develop effective risk management strategies. The importance and implications of variance in the context of the EWMA cannot be overstated, as it forms the basis for reliable forecasting and sound decision-making.

Understanding the Variance of EWMA

In the field of finance, risk management is of utmost importance. One of the commonly used techniques for measuring and managing risk is the Exponentially Weighted Moving Average (EWMA) model. EWMA is a statistical method that allows for the calculation of a weighted average of historical data, giving more weight to recent observations and less weight to older observations.

While the focus of many studies and discussions surrounding EWMA has been on its mean or expected value, the variance of EWMA is equally important. Understanding the variance of EWMA can provide insights into the stability and reliability of the model. It is also crucial for accurately estimating confidence intervals and making informed decisions based on the risk measures derived from EWMA.

The variance of EWMA is influenced by various factors, including the choice of the decay factor or smoothing constant, the length of the time series data used, and the underlying distribution of the data. A higher decay factor or shorter time series will result in a smaller variance, indicating a more responsive and volatile model. Conversely, a lower decay factor or longer time series will lead to a larger variance, suggesting a smoother and less volatile model.

To gain a deeper understanding of the variance of EWMA, it is useful to examine its implications. A low variance indicates a more stable and predictable model, which may be preferred in risk management applications where stability and predictability are crucial. On the other hand, a high variance suggests a more volatile and uncertain model, which may be suitable for scenarios where more flexibility and adaptability are desired.

Furthermore, the variance of EWMA plays a significant role in estimating confidence intervals for risk measures such as Value-at-Risk (VaR) and Expected Shortfall (ES). A smaller variance will result in narrower confidence intervals, indicating a higher level of confidence in the estimated risk measures. Conversely, a larger variance will lead to wider confidence intervals, signifying more uncertainty in the estimated risk measures.

Read Also: Understanding Forex Volume Profile: Key Insights and Analysis

In conclusion, understanding the variance of EWMA is essential for accurately assessing and managing risk. It provides insights into the stability and reliability of the model, helps in making informed decisions based on risk measures, and plays a crucial role in estimating confidence intervals. By considering the variance of EWMA alongside its mean, practitioners and researchers can gain a more comprehensive understanding of the model and its implications in a risk management context.

Exploring the Importance of Variance in EWMA

Exponentially Weighted Moving Average (EWMA) is a popular method in statistics and finance for calculating the smoothed average of a data series over time. While the primary focus is typically on the mean or average value, the variance of the data is also a critical aspect to consider.

Variance measures the variability or dispersion of the data points around the mean. A higher variance implies a wider range of values, indicating greater volatility or uncertainty in the data. In the context of EWMA, understanding the variance is vital for several reasons.

Firstly, variance provides insights into the stability of the data series. A low variance indicates that the data points are closely clustered around the mean, suggesting a relatively stable and predictable pattern. On the other hand, a high variance suggests that the data points are more scattered, indicating a greater level of unpredictability and potential risk.

Read Also: Is it legal to trade in dollars in Ghana? Exploring the legal provisions

Secondly, variance is crucial in risk management. In finance, volatility is a key measure of risk, and variance is directly related to volatility. By considering the variance in EWMA, financial analysts and traders can assess the level of risk associated with a particular asset or portfolio. This information can be used to make informed investment decisions and manage risk effectively.

Furthermore, variance plays a significant role in determining the weights assigned to each data point in the EWMA calculation. In EWMA, more recent data points are assigned higher weights, while older data points are given lower weights. The selection of appropriate weights is critical for achieving an accurate and responsive smoothing effect. By taking into account the variance, analysts can adjust the weights to reflect the level of confidence or uncertainty in the data, leading to more reliable and meaningful results.

Overall, understanding the importance of variance in EWMA is essential for effectively analyzing and interpreting the results. By considering the variance, one can gain valuable insights into the stability of the data, assess the level of risk, and optimize the smoothing effect. Therefore, it is crucial to incorporate variance into the analysis to make informed decisions and mitigate potential risks.

FAQ:

What is EWMA and how is it used in finance?

EWMA stands for Exponentially Weighted Moving Average. It is a statistical method used in finance to calculate the volatility of an asset’s returns. It gives more weight to recent data points, making it more responsive to changes in market conditions.

Why is understanding the variance of EWMA important?

Understanding the variance of EWMA is important because it helps investors and financial analysts assess the risk and volatility of a particular asset. By knowing the variance, they can make informed decisions regarding portfolio management, risk assessment, and trading strategies.

How is the variance of EWMA calculated?

The variance of EWMA is calculated by multiplying the square of the previous day’s EWMA volatility by a decay factor and adding it to the square of the current day’s return. The decay factor determines the weight given to the previous day’s volatility. The resulting sum is then multiplied by a weighting factor to give the final variance.

What are the implications of having a high variance of EWMA?

A high variance of EWMA implies that the asset’s returns have been more volatile and unpredictable. This may indicate a higher level of risk associated with the asset, making it a potentially riskier investment. It can also suggest that the asset’s returns are influenced by external factors and market conditions, rather than following a predictable pattern.

Can the variance of EWMA be used to forecast future volatility?

Yes, the variance of EWMA can be used to forecast future volatility. By analyzing the historical volatility and trends in the variance, investors and analysts can make predictions about the future volatility of an asset. This information can be valuable in developing trading strategies, managing risk, and making investment decisions.

What is EWMA?

EWMA stands for Exponentially Weighted Moving Average. It is a statistical method used to calculate the average of a series of data points over time, with more weight given to recent observations.