Understanding the Distinctions between Moving Average and Savitzky-Golay Filter

Understanding the Difference between Moving Average and Savitzky-Golay Filter

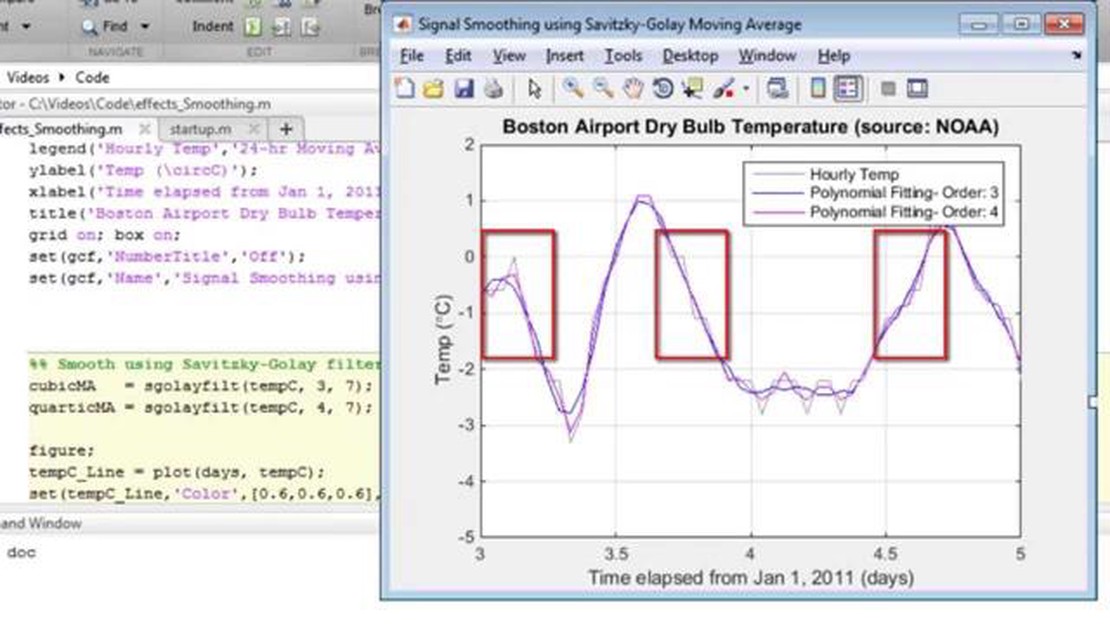
In the field of signal processing, there are various methods used for data smoothing and noise reduction. Two commonly used techniques are the Moving Average and Savitzky-Golay Filter. While both methods aim to achieve similar results, there are important distinctions between them that are worth understanding.

The Moving Average is a simple and intuitive filter that calculates the average of a series of data points within a specified window. This window slides through the data, and the average value at each position becomes the smoothed value at that position. This method is effective in reducing high-frequency noise, but it may blur sharp transitions and introduce lag in the filtered signal.

Table Of Contents

On the other hand, the Savitzky-Golay Filter is a more advanced technique that utilizes polynomial fitting to smoothen data. Instead of using a fixed window to calculate the average, this filter fits a polynomial function to a small section of the data, which is then used to estimate the smoothed value at each point. Unlike the Moving Average, the Savitzky-Golay Filter can preserve details and sharp edges in the data while effectively reducing noise.

Another key distinction between the two methods lies in their ability to handle different types of noise. While the Moving Average is suitable for random noise, it may struggle with systematic noise patterns. The Savitzky-Golay Filter, however, can handle both random and systematic noise, making it a more versatile option in many cases.

Conclusion:

Both the Moving Average and Savitzky-Golay Filter are valuable tools in signal processing, but they have distinct characteristics that make them suitable for different scenarios. The Moving Average is simple and effective, but it may blur details and introduce lag. The Savitzky-Golay Filter, on the other hand, can preserve details while reducing noise, making it a more versatile option. Understanding the distinctions between these methods allows for better decision-making when it comes to choosing the most appropriate filter for a specific application.

Definition and Application of Moving Average Filter

The moving average filter, often abbreviated as MA filter, is a widely used signal processing technique that smooths out fluctuations in data by calculating the average of a sequence of adjacent data points. It is based on the principle that a moving average filter can estimate the trend or pattern in a data set by averaging a subset of the data at each point in time.

The moving average filter works by sliding a window of a fixed size across a time series data set. At each step, the filter calculates the average of the data points within the window and replaces the central value with this average. The window size, also known as the order of the filter, determines the number of adjacent data points that are considered in the calculation. A larger window size results in a smoother output, while a smaller window size preserves more details of the original data.

The moving average filter is commonly used in various fields including finance, economics, and engineering. It is often applied to remove noise or to smooth out fluctuations in time series data such as stock prices, economic indicators, or sensor measurements. The filter can be used as a preprocessing step before further analysis or as a standalone tool for data visualization or trend analysis.

One of the advantages of the moving average filter is its simplicity and ease of implementation. It does not require complex mathematical calculations and can be easily understood and used by individuals with varying levels of technical expertise. Additionally, the moving average filter provides a flexible approach as the window size can be adjusted to balance between noise reduction and preserving important features in the data.

However, the moving average filter also has limitations. It can introduce a lag in the filtered data, meaning that the filtered output is shifted in time compared to the original input. This lag can be problematic in applications that require real-time or near-real-time analysis. Additionally, the filter is sensitive to outliers or abrupt changes in the data, as it treats all data points within the window equally without considering their individual weights or significance.

Read Also: Understanding derivative products and their importance in finance

In conclusion, the moving average filter is a widely used signal processing technique for smoothing and analyzing time series data. It provides a simple and intuitive approach to remove noise and estimate the trend in a data set. While it has limitations, understanding its definition and application can help researchers and practitioners make informed decisions when choosing the appropriate filter for their data analysis tasks.

Definition and Application of Savitzky-Golay Filter

The Savitzky-Golay filter is a digital signal processing technique used for smoothing and noise reduction of time series data. Unlike the moving average filter, which calculates the average of a window of data points, the Savitzky-Golay filter uses a least squares polynomial fitting algorithm to estimate the underlying trend of the data.

By fitting a polynomial function to the data within a sliding window, the Savitzky-Golay filter can effectively remove noise and preserve the important features of the signal. The filter achieves this by estimating the polynomial coefficients in such a way that the least squares error between the fitted polynomial and the original data is minimized.

The Savitzky-Golay filter has a number of applications in various fields. It is commonly used in signal processing, particularly in the analysis of noisy time series data. It can be applied to smooth out data from sensors or instruments that are affected by random fluctuations or measurement errors.

Read Also: Is Forex Trading Allowed in the USA? Understanding the Regulations

In addition to noise reduction, the Savitzky-Golay filter can also be used for derivative estimation. By fitting a high-order polynomial to the data, the filter can estimate the slope or rate of change of the signal at each point. This makes the filter useful in applications such as signal differentiation, peak detection, and peak width estimation.

Overall, the Savitzky-Golay filter is a powerful tool for smoothing and analyzing time series data. Its ability to remove noise while preserving important features makes it a valuable technique in various fields, ranging from scientific research to industrial process monitoring.

FAQ:

What is a moving average filter?

A moving average filter is a widely used digital signal processing technique that filters out random noise from a data set by calculating the average of a specified number of data points within a sliding window.

How does a moving average filter work?

A moving average filter works by sliding a window of fixed size over the data set and calculating the average of the data points within the window. This window is then moved along the data set, and for each position, a new average is calculated.

What are the advantages of using a moving average filter?

The advantages of using a moving average filter include noise reduction, smoothing of data, and the ability to emphasize or suppress certain frequency components depending on the chosen window size.

What is a Savitzky-Golay filter?

A Savitzky-Golay filter is a type of digital filter that is used to smooth and differentiate data. It is based on a least squares polynomial fitting approach and provides better control over the trade-off between noise reduction and signal preservation compared to a moving average filter.

How does a Savitzky-Golay filter differ from a moving average filter?

A Savitzky-Golay filter differs from a moving average filter in that it uses a least squares polynomial fitting approach instead of simply averaging data points. This allows it to better preserve the shape of the underlying signal while still reducing noise.

What is a moving average filter?

A moving average filter is a technique used to smooth out a time series data by calculating the average of a specific number of adjacent data points.

How does a moving average filter work?

A moving average filter works by sliding a window of a specific size across a time series data, calculating the average of the data points within the window, and replacing the central data point with the calculated average.