Understanding the Distinctions Between ARIMA and VARMA Models

What is the difference between ARIMA and VARMA?

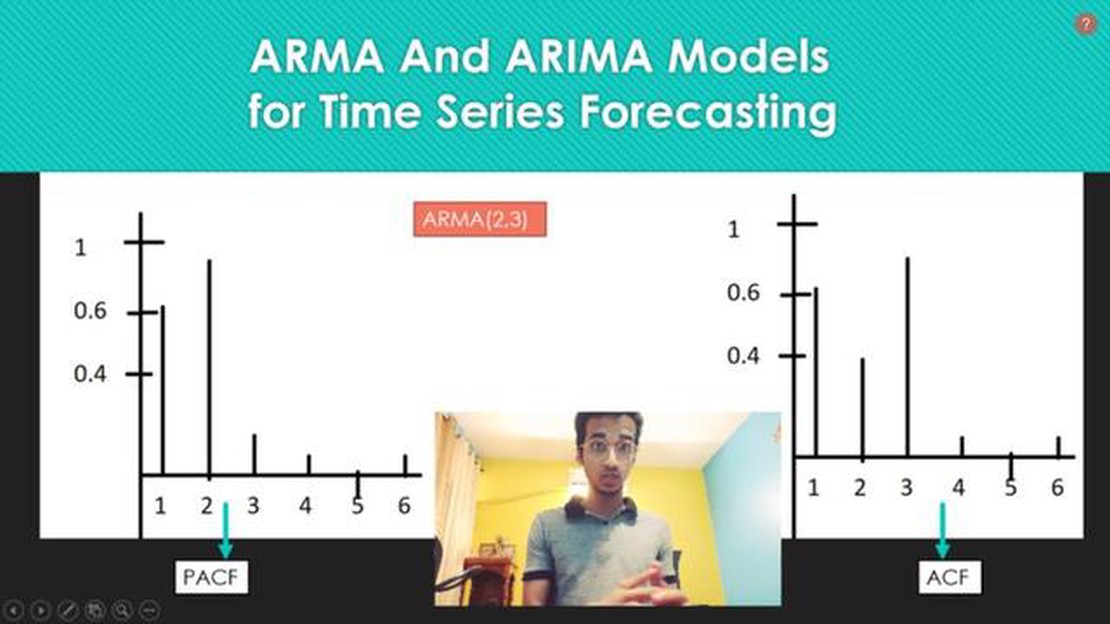
In the field of time series analysis, two commonly used models for forecasting and understanding the behavior of complex systems are the ARIMA (Autoregressive Integrated Moving Average) model and the VARMA (Vector Autoregressive Moving Average) model. While both models are valuable tools for analyzing time series data, they have distinct differences in their structure and applications.

Table Of Contents

The ARIMA model is a univariate model, meaning it is used to analyze and forecast a single time series variable. It is a combination of three components: the autoregressive (AR) component, the differencing (I) component, and the moving average (MA) component. The AR component captures the linear relationship between an observation and a certain number of lagged observations, while the MA component captures the linear relationship between an observation and a certain number of lagged forecast errors. The differencing component is used to make the time series stationary by subtracting the previous observation from the current observation. ARIMA models are widely used in fields such as finance, economics, and climate science.

The VARMA model, on the other hand, is a multivariate model that can capture the relationships between multiple time series variables. It is an extension of the ARMA model, which combines the AR and MA components. The VARMA model allows for the analysis of complex systems with feedback loops, where the variables interact with each other over time. This model is useful in a wide range of fields including macroeconomics, social sciences, and engineering.

While both ARIMA and VARMA models can be used to forecast future values and understand the dynamics of time series data, it is important to choose the appropriate model based on the nature of the data and the research question at hand. ARIMA models are suitable for analyzing and forecasting univariate data, while VARMA models are more appropriate when analyzing the relationships between multiple variables. Understanding the distinctions between these models is crucial for effectively applying time series analysis techniques in various domains.

Overview of ARIMA Models

ARIMA (Autoregressive Integrated Moving Average) models are powerful and widely used time series models that are commonly employed in forecasting tasks. These models are capable of capturing the nonlinear dynamics and dependencies in time series data, making them valuable tools in various fields such as finance, economics, and meteorology.

The ARIMA model consists of three main components: the autoregressive (AR) component, the integrated (I) component, and the moving average (MA) component.

The autoregressive (AR) component accounts for the linear relationship between the current value of the time series and its past values. It models the dependence of a variable on its own previous values.
The integrated (I) component deals with the differencing of the time series in order to make it stationary. Stationarity is an important assumption in time series analysis, as it ensures that the statistical properties of the series do not change over time.
The moving average (MA) component represents the linear relationship between the current value of the time series and the residual errors from previous time steps. It captures the short-term dependencies in the time series data.

ARIMA models are typically denoted as ARIMA(p, d, q), where p represents the order of the autoregressive component, d represents the order of differencing, and q represents the order of the moving average component. The selection of appropriate values for these parameters requires careful analysis of the time series data and the identification of its underlying patterns and characteristics.

By fitting the ARIMA model to historical data and estimating its parameters, we can obtain forecasts for future time steps. These forecasts can be used for a wide range of applications, including predicting stock prices, forecasting demand for products, and estimating future economic indicators.

Despite their usefulness, ARIMA models have some limitations. They assume that the underlying data follows a specific pattern, and may not perform well if the data exhibits nonlinear dependencies or if there are outliers present. Additionally, ARIMA models are often sensitive to the selection of model parameters, and choosing inappropriate values can lead to inaccurate forecasts.

Read Also: Learn the Basics of Online Forex Trading for Beginners

Nevertheless, with proper understanding and careful analysis, ARIMA models can provide valuable insights and accurate forecasts for a wide range of time series data.

Overview of VARMA Models

Vector Autoregressive Moving Average (VARMA) models are a class of time series models that combine autoregressive (AR) and moving average (MA) components with multiple time series variables. Unlike univariate ARIMA models, VARMA models can capture the dynamics and relationships between multiple variables simultaneously.

In a VARMA model, each time series variable is modeled as a linear combination of its own lagged values and the lagged values of other variables in the system. This allows the model to incorporate the interdependencies and feedback effects among the variables.

A VARMA model is specified by two main components: the autoregressive part (VAR) and the moving average part (MA). The VAR component captures the dependence of each variable on its own lagged values and the lagged values of other variables. The MA component captures the dependence of each variable on the lagged values of the error terms from the VAR component.

Read Also: Choosing the Best Technical Indicator for Intraday Trading: A Comprehensive Guide

The order of a VARMA model is represented as (p, q, s), where p denotes the order of the VAR component, q denotes the order of the MA component, and s denotes the number of time steps between observations. The p, q, and s values are determined through model estimation and selection techniques, such as information criteria or likelihood-based methods.

VARMA models are commonly used in various fields, including economics, finance, and engineering, to analyze and forecast multivariate time series data. They offer a flexible framework to capture the complex dynamic relationships among variables and can provide valuable insights into the behavior of a system over time.

FAQ:

What is the difference between ARIMA and VARMA models?

ARIMA models are used for time series forecasting, while VARMA models are used for multivariate forecasting.

Can an ARIMA model be used for multivariate forecasting?

No, ARIMA models can only handle univariate time series data.

What does ARIMA stand for?

ARIMA stands for Autoregressive Integrated Moving Average.

Are ARIMA and VARMA models suitable for predicting stock prices?

Yes, both ARIMA and VARMA models can be used for predicting stock prices, but VARMA models are more suitable for modeling the dependencies among multiple stocks.