What is the formula for zero-phase filter? - Everything you need to know

What is the formula for zero-phase filter?

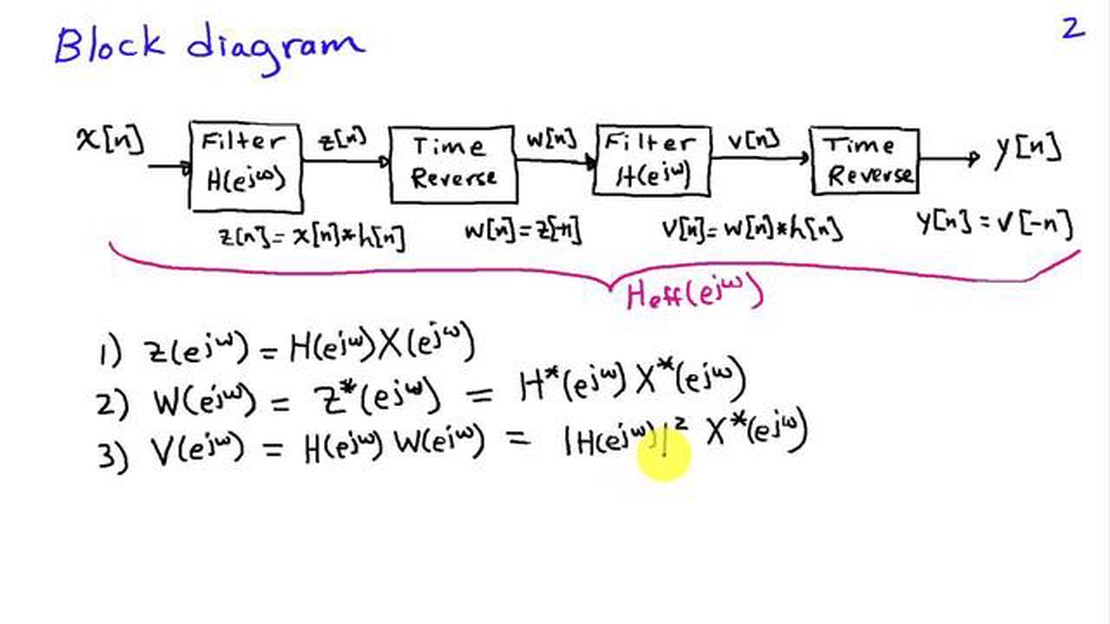
Zero-phase filters play a crucial role in various areas of signal processing and digital filtering. These filters are designed to remove any phase distortion introduced by a filter while preserving the amplitude characteristics of the original signal. In other words, a zero-phase filter provides a linear phase response, ensuring that all frequencies in the signal are delayed by the same amount.

Table Of Contents

The formula for calculating a zero-phase filter depends on the specific type of filter being used. One common type is the FIR (Finite Impulse Response) filter, which is a digital filter with a finite impulse response. The formula for a zero-phase FIR filter involves designing the filter coefficients in such a way that the filter response is symmetric and has linear phase characteristics.

Another type of zero-phase filter is the IIR (Infinite Impulse Response) filter, which is a digital filter with an infinite impulse response. The formula for a zero-phase IIR filter is more complex and typically involves using techniques such as the butterworth or chebyshev filter design methods to achieve the desired zero-phase response.

Overall, understanding the formula for a zero-phase filter is essential for engineers and researchers working in fields such as audio signal processing, image processing, and telecommunications. By applying the appropriate formula and design techniques, one can create filters that effectively remove phase distortion while preserving the integrity of the original signal.

Understanding the Zero-Phase Filter: A Comprehensive Guide

The zero-phase filter is a powerful tool in the field of signal processing that eliminates phase distortion in a signal. It is widely used in various applications, including audio processing, image processing, and digital communications.

So, what exactly is a zero-phase filter? It is a type of filter that achieves the important property of zero phase shift. In other words, when a signal is passed through a zero-phase filter, it does not introduce any delay or phase shift to the signal.

This is particularly useful in applications where maintaining the temporal alignment of the signal is critical. For example, in audio processing, zero-phase filters are used to remove unwanted noise or enhance certain frequency components without introducing any delays.

The main advantage of zero-phase filters is their ability to preserve the time-domain characteristics of a signal. This means that the filtered signal will retain the same shape and timing as the original signal, but with the desired modifications applied.

One common implementation of zero-phase filters is the use of finite impulse response (FIR) filters. These filters are designed based on a finite set of coefficients, and their impulse response is of finite duration. FIR filters can be designed to achieve zero-phase characteristics by employing symmetric coefficients, with the filter’s output being the sum of delayed versions of the input signal multiplied by the coefficients.

Another approach involves using minimum-phase filters, which are filters that have a minimum phase shift for a given magnitude response. By cascading a minimum-phase filter with its reverse minimum-phase counterpart, a zero-phase filter can be created.

It is important to note that while zero-phase filters offer significant benefits, they are not without limitations. Due to the requirement for symmetry or cascading of minimum-phase filters, there is often a trade-off between the sharpness of the frequency response and the length of the filter.

In conclusion, the zero-phase filter is a powerful tool that allows for phase distortion-free signal processing. With the ability to preserve the time-domain characteristics of a signal, it finds applications in various fields. Understanding the principles and implementation methods of zero-phase filters is essential for anyone working in the field of signal processing.

What is a Zero-Phase Filter?

A zero-phase filter is a type of digital filter that does not introduce any phase shift or delay in the filtered signal. In other words, it preserves the relative timing of the different frequency components in the input signal.

Read Also: British Dollar to PKR: Latest Currency Exchange Rate

Unlike other types of filters, which introduce a certain amount of phase distortion, zero-phase filters ensure that the output signal is aligned in time with the input signal. This can be particularly important in applications where preserving the phase relationship between different frequencies is critical, such as in audio processing and image processing.

Zero-phase filters are commonly used in various signal processing applications. They can be implemented using different techniques, such as finite impulse response (FIR) filters and infinite impulse response (IIR) filters. FIR filters are often preferred for zero-phase filtering because they have symmetric impulse responses, which means that the phase distortion introduced by the filter is the same in both the forward and reverse directions.

Read Also: Is Part-Time Forex Trading Possible? 5 Key Considerations

It is worth noting that while zero-phase filters can effectively remove unwanted frequencies from a signal without introducing phase distortion, they do not provide perfect frequency selectivity. This means that there may still be some signal leakage into adjacent frequency bands, especially in cases where the filter has a wide passband.

In summary, a zero-phase filter is a type of digital filter that preserves the relative timing of different frequency components in a signal. It is commonly used in audio and image processing applications where phase accuracy is important.

How Does a Zero-Phase Filter Work?

A zero-phase filter is a type of digital filter that removes or attenuates certain frequencies from a signal while maintaining a constant phase shift of zero degrees. Unlike other types of filters, a zero-phase filter does not introduce any phase distortion to the signal, meaning it does not change the timing or alignment of different frequency components.

The basic principle behind a zero-phase filter is to apply a phase shift that cancels out any phase distortion introduced by the filter’s frequency response. This is done by carefully designing the filter coefficients or transfer function so that the phase response is symmetrical with respect to the desired zero-phase frequency. The symmetric phase response ensures that the filter introduces an equal and opposite phase shift, effectively canceling out any phase distortion.

Zero-phase filters are commonly used in various applications, including audio processing, image processing, and telecommunications. In audio processing, for example, a zero-phase filter can be used to remove unwanted noise or enhance specific frequency components without altering the timing or phase relationships of the audio signal.

There are different methods and algorithms for designing zero-phase filters, including finite impulse response (FIR) filters and infinite impulse response (IIR) filters. Each design method has its advantages and limitations, and the choice depends on the specific application requirements.

Overall, zero-phase filters are powerful tools for signal processing that allow for precise control over frequency components while maintaining a constant phase relationship. By eliminating phase distortion, these filters enable accurate and reliable analysis, manipulation, and enhancement of signals in various fields of technology and science.

FAQ:

What is a zero-phase filter?

A zero-phase filter is a type of filter that doesn’t introduce any phase shifts or delays to the filtered signal. It maintains the phase relationships of the different frequency components of the input signal, resulting in a filter output that is in phase with the original signal.

How does a zero-phase filter work?

A zero-phase filter works by employing a forward and backward filtering process. The input signal is first filtered in the forward direction, and then the filtered signal is reversed in time and filtered again in the backward direction. This ensures that any phase shifts introduced by the filtering process are cancelled out, resulting in a zero-phase filter output.

What are the applications of zero-phase filters?

Zero-phase filters are commonly used in a variety of applications, such as audio signal processing, seismic signal processing, and image processing. They are especially useful in situations where maintaining the phase relationships of the signal is important, such as in audio equalization or signal analysis.

What is the formula for a zero-phase filter?

The formula for a zero-phase filter depends on the specific type of filter used. For example, a common type of zero-phase filter is the symmetric FIR filter, which can be implemented using the following formula: y[n] = b0x[n] + b1x[n-1] + … + bm*x[n-m]

What are the advantages of using a zero-phase filter?

One of the main advantages of using a zero-phase filter is that it preserves the phase relationships of the different frequency components of the input signal. This can be important in applications such as audio signal processing, where maintaining the phase coherence of the signal is crucial for preserving the spatial and timbral qualities of the sound.