Understanding the Impact of Shifting Data on Standard Deviation

How does shifting data affect standard deviation?

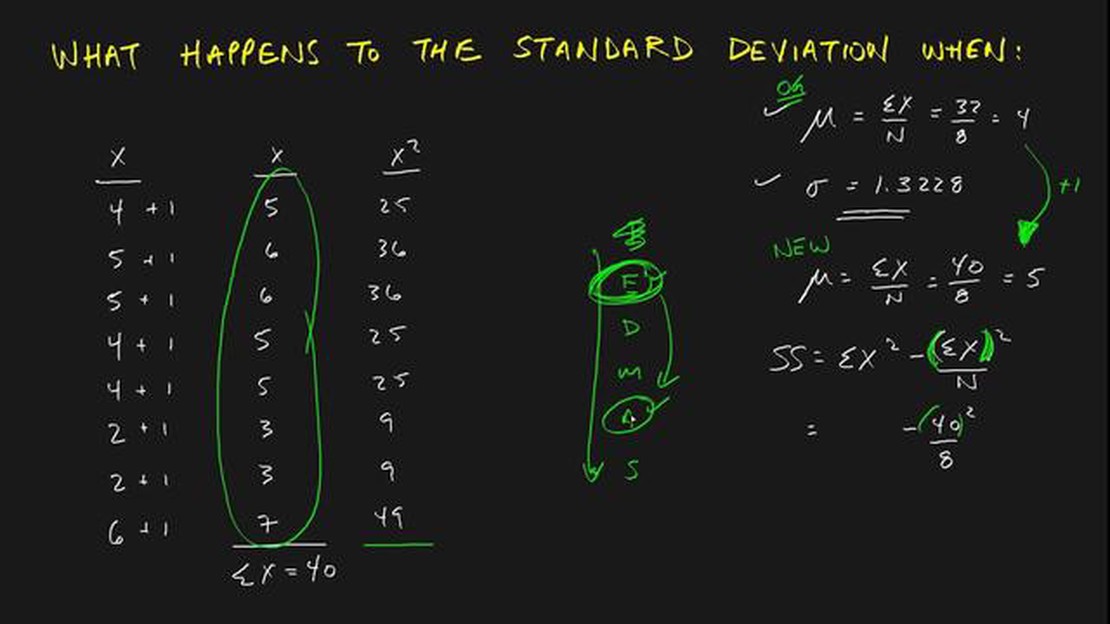
The standard deviation is a statistical measure that quantifies the amount of variability or dispersion in a dataset. It provides valuable insights into the spread of data points around the mean or average. However, what happens when the dataset undergoes a shift? How does this affect the standard deviation?

Table Of Contents

When the data undergoes a shift, such as a change in the mean or the introduction of outliers, the standard deviation is also affected. In particular, the measure becomes more sensitive to extreme values and may increase or decrease depending on the shift. This is because the standard deviation is calculated using the squared differences between each data point and the mean. When there is a shift, these differences are altered, thereby influencing the resulting standard deviation value.

Let’s take an example to better understand this concept. Consider a dataset of employee salaries before and after a pay raise. If the mean salary increases after the raise, the standard deviation may also increase. This is because the differences between each salary and the new mean are likely to be larger than before the shift. On the other hand, if the new mean is lower than the previous mean, the standard deviation may decrease since the differences are smaller. In both cases, the shift in data impacts the calculation and interpretation of the standard deviation.

“The measure of standard deviation is a powerful tool in understanding the variability within a dataset. However, it is crucial to consider the impact of shifting data on its calculation and interpretation. By recognizing how shifts are reflected in standard deviation values, we can make more informed conclusions and decisions based on our data.”

Exploring the Relationship between Data Shift and Standard Deviation

In statistical analysis, the standard deviation is a measure of the dispersion or spread of a dataset. It provides valuable insights into the variability and volatility of the data points. However, one factor that can significantly impact the standard deviation is the shifting of data.

Data shifting refers to the process of moving the entire dataset up or down, resulting in a change in the mean of the data. When the data is shifted, the standard deviation can either increase or decrease, depending on the direction of the shift and the distribution of the data points.

When the data is shifted upwards (increasing the mean), the standard deviation tends to increase as well. This is because the data points are now further away from the new mean, resulting in a higher spread. On the other hand, when the data is shifted downwards (decreasing the mean), the standard deviation tends to decrease. The data points are now closer to the new mean, leading to a lower spread.

It’s important to note that the impact of data shifting on the standard deviation also depends on the shape of the distribution. In symmetrical distributions like the normal distribution, shifting the data in either direction will have a similar impact on the standard deviation. However, in skewed distributions, the effect of shifting can be more pronounced.

Understanding the relationship between data shift and standard deviation is crucial for interpreting statistical analysis results correctly. When analyzing datasets that have undergone data shifting, it is important to consider both the mean and the standard deviation to get a comprehensive understanding of the dataset’s characteristics.

In conclusion, data shifting can significantly impact the standard deviation of a dataset. The direction of the shift and the distribution’s shape play a crucial role in determining whether the standard deviation increases or decreases. Considering both the mean and the standard deviation is essential for accurate statistical analysis.

The Significance of Data Distribution in Standard Deviation Calculation

Standard deviation is a statistical measure of the dispersion or variability of a dataset. It quantifies the amount of variation or deviation from the average or mean. When calculating the standard deviation, it is important to consider the distribution of the data.

Read Also: Is AvaTrade a Legit Broker? Expert Analysis and Review

The distribution of data refers to how the values are spread out across the dataset. It can take various forms, including normal distribution, skewed distribution, or bimodal distribution. The shape of the distribution affects the value of the standard deviation.

In a normal distribution, the data is symmetrically distributed around the mean, resulting in a bell-shaped curve. In this case, the standard deviation provides a good representation of the spread of the data. A higher standard deviation indicates a wider spread, while a lower standard deviation suggests a narrower spread.

However, in skewed distributions, where the data is not evenly distributed, the standard deviation may not accurately represent the spread. For example, in a positively skewed distribution, where the tail of the curve extends towards higher values, the standard deviation may be larger than expected. This is because the presence of outliers or extreme values in the tail increases the variability.

On the other hand, in a bimodal distribution, where the data has two distinct peaks, the standard deviation may not capture the nature of the distribution accurately. In these cases, it is important to consider other measures of variability or to analyze the dataset separately.

Read Also: Changing money at Osuuspankki: Everything you need to know

Understanding the distribution of the data is crucial for interpreting the standard deviation. It helps in assessing the reliability of the standard deviation as a measure of dispersion. Additionally, it allows for a more comprehensive interpretation of the dataset and the characteristics of the data points.

Overall, the significance of data distribution in standard deviation calculation lies in its ability to provide insight into the spread of the dataset and the reliability of the measure. It helps in gaining a deeper understanding of the data distribution and its impact on statistical analysis.

FAQ:

What is standard deviation?

Standard deviation is a statistical measure that quantifies the amount of variation or dispersion in a dataset.

How is standard deviation calculated?

Standard deviation is calculated by taking the square root of the variance. The variance is calculated by taking the average of the squared differences between each data point and the mean of the dataset.

Why is standard deviation important?

Standard deviation is important because it provides a measure of how spread out the values in a dataset are. It helps in understanding the variability and distribution of the data.

What is the impact of shifting data on standard deviation?

Shifting data can have a significant impact on the standard deviation. If the data is shifted towards higher or lower values, the standard deviation will increase as it measures the dispersion from the mean.

How does a larger standard deviation affect the interpretation of data?

A larger standard deviation indicates that the data points are more spread out from the mean. This means that there is more variability in the dataset, which can affect the interpretation and generalization of the data.

What is standard deviation?

Standard deviation is a statistical measure that quantifies the amount of variation or dispersion in a set of data values.

How is standard deviation calculated?

Standard deviation is calculated by finding the square root of the variance of a set of data. The variance is calculated by taking the average of the squared differences between each data point and the mean.