Learn how to calculate a correlation matrix step-by-step

How to calculate correlation matrix?

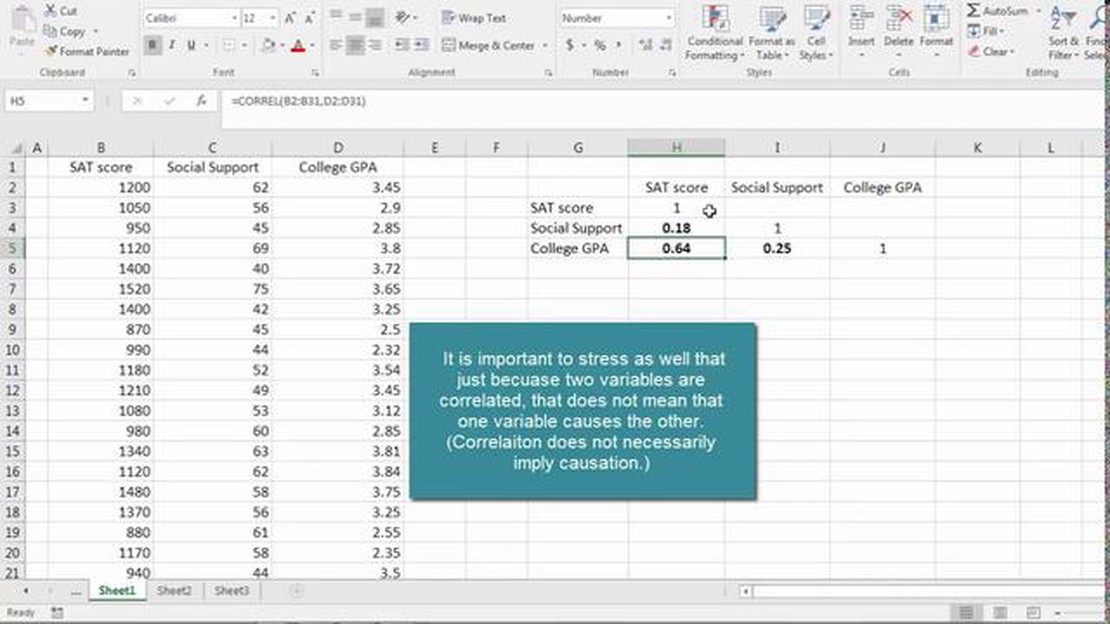
Correlation is a statistical measure that quantifies the relationship between two variables. It helps us understand how changes in one variable are related to changes in another variable. Calculating a correlation matrix is a useful technique in data analysis as it helps identify patterns and relationships between multiple variables.

Table Of Contents

To calculate a correlation matrix, follow these steps:

Collect your data: Before you can calculate a correlation matrix, you need to gather the data for the variables you want to analyze. Make sure you have numerical data for each variable.
Calculate the correlation coefficient: The correlation coefficient measures the strength and direction of the relationship between two variables. There are different types of correlation coefficients, such as Pearson’s correlation coefficient and Spearman’s rank correlation coefficient. Choose the appropriate one based on the type of data you have.
Create a matrix: To create a correlation matrix, you need to organize your data in a clear and systematic way. Create a table or spreadsheet with the variables as columns and the observations as rows.
Calculate the correlation: Using the correlation coefficient formula, calculate the correlation between each pair of variables. This involves comparing the values of the variables and applying the appropriate formula.
Fill in the matrix: Record the calculated correlation coefficients in the appropriate cells of the correlation matrix. Each coefficient represents the correlation between the corresponding pair of variables.

Remember, interpreting the correlation matrix requires understanding the context of your data and the variables being analyzed. A high positive correlation indicates a strong positive relationship between variables, while a high negative correlation indicates a strong negative relationship. A correlation coefficient close to zero suggests a weak or no relationship.

Calculating a correlation matrix step-by-step allows you to explore the relationships between variables and gain insights into your data. It is an essential tool for data analysts, statisticians, and researchers, providing valuable information for decision-making and further analysis.

What is a correlation matrix?

A correlation matrix is a table that displays the correlation coefficients between a set of variables. It is commonly used in statistics and data analysis to examine the strength and direction of the linear relationship between variables. The correlation coefficient measures the extent to which two variables are related to each other.

The correlation matrix is a square matrix, where each row and column represents a different variable. The diagonal elements of the matrix are always equal to 1, as they represent the correlation between a variable and itself. The off-diagonal elements represent the correlation between two different variables. The correlation coefficient can range from -1 to 1, with -1 indicating a perfect negative correlation, 1 indicating a perfect positive correlation, and 0 indicating no correlation.

Read Also: Understanding Forex Switching: A Guide for Traders

A correlation matrix can be used to identify patterns and relationships in a dataset. It can help researchers understand how variables are related to each other and identify potential variables to include or exclude in statistical models. The correlation matrix can also be visualized using heatmaps or scatterplots, which provide a graphical representation of the correlation coefficients.

In summary, a correlation matrix is a useful tool for analyzing the relationship between variables. It provides a comprehensive overview of the correlations between a set of variables and can help researchers make informed decisions during data analysis.

How to calculate a correlation matrix step-by-step

A correlation matrix is a table that shows the correlation coefficients between multiple variables. It is used to understand the relationship between different variables and to identify patterns and trends in data. Here is a step-by-step guide on how to calculate a correlation matrix:

Identify the variables: Determine the variables for which you want to calculate the correlation matrix. These variables should be numeric and continuous in nature.
Create a data matrix: Organize your data into a matrix format, where each row represents an observation and each column represents a variable. Make sure the variables are properly labeled.
Calculate the correlation coefficients: Use a statistical software or programming language to calculate the correlation coefficients for all pairs of variables. The most common correlation coefficient is Pearson’s correlation coefficient, which measures the linear relationship between two variables.
Construct the correlation matrix: Create a square matrix where the rows and columns represent the variables. Enter the calculated correlation coefficients into the corresponding cells of the matrix.
Interpret the correlation matrix: Analyze the correlation matrix to understand the relationships between the variables. Positive values indicate a positive linear relationship, negative values indicate a negative linear relationship, and values close to zero indicate no linear relationship.

Calculating a correlation matrix can help in various fields such as finance, economics, psychology, and epidemiology. It provides insights into the strength and direction of relationships between variables, which can be used to make informed decisions and predictions.

Read Also: Why did the Canucks trade Luongo? Unveiling the reasons behind the trade

FAQ:

What is a correlation matrix?

A correlation matrix is a table that displays the correlation coefficients between multiple variables in a dataset. It shows how the variables are related to each other.

How is a correlation coefficient calculated?

A correlation coefficient is a numerical value that represents the strength and direction of the relationship between two variables. It is calculated by dividing the covariance of the two variables by the product of their standard deviations.

Why is the correlation matrix useful?

The correlation matrix is useful because it provides a quick and easy way to visualize the relationships between multiple variables. It can help identify patterns and dependencies in the data.

How do you interpret a correlation coefficient?

The correlation coefficient ranges from -1 to 1. A value of 1 indicates a perfect positive correlation, -1 indicates a perfect negative correlation, and 0 indicates no correlation. The closer the value is to 1 or -1, the stronger the correlation.

What are some limitations of the correlation matrix?

One limitation is that correlation does not imply causation. Just because two variables are strongly correlated does not mean that one variable causes the other. Another limitation is that the correlation matrix only measures linear relationships and may not capture other types of relationships.