Why is the expectation of Brownian motion 0?

Why is the expectation of Brownian motion 0?

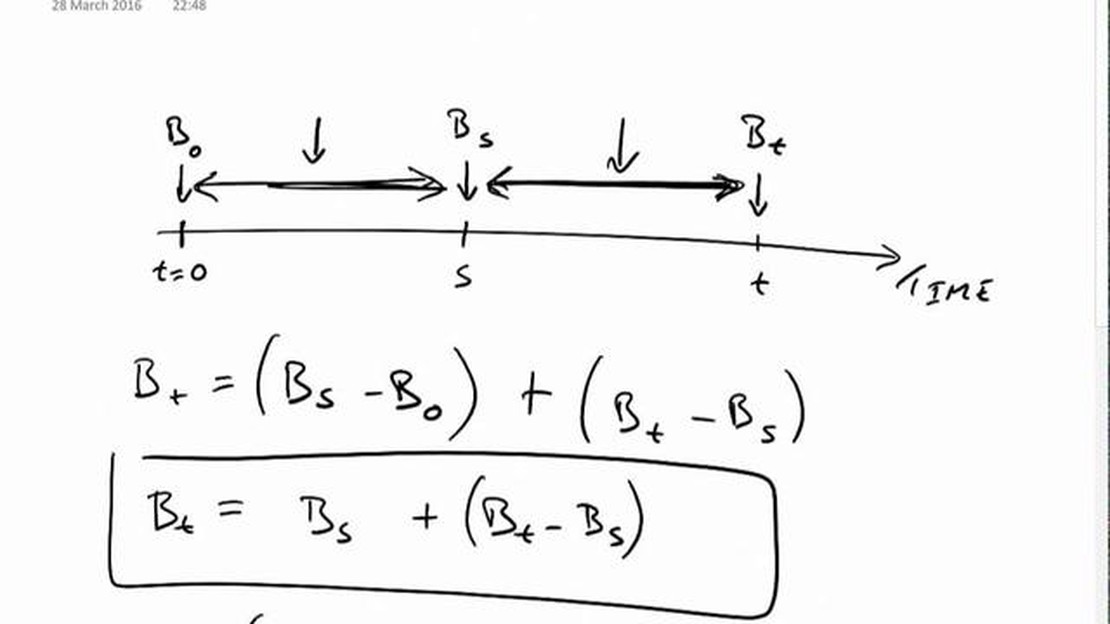
Brownian motion is a continuous random walk that is widely used in many areas of science, including physics, finance, and engineering. It is named after the Scottish botanist Robert Brown, who observed the erratic movement of pollen particles suspended in liquid.

One of the key properties of Brownian motion is that its expectation, or average value, is always equal to zero. This means that on average, the motion does not have any tendency to move in a particular direction.

Table Of Contents

The expectation of Brownian motion being zero can be understood intuitively by considering the random nature of its movements. Since Brownian motion is driven by random forces, the motion is equally likely to move in any direction. Therefore, over a large number of steps, the positive and negative movements will cancel each other out, resulting in an average value of zero.

Mathematically, the expectation of Brownian motion being zero can be derived from its defining property as a martingale. A martingale is a sequence of random variables that satisfies a certain consistency condition. The expectation of a martingale at any given time is equal to its initial value. Since the initial value of Brownian motion is zero, its expectation at any time is also zero.

Overall, the expectation of Brownian motion being zero is a fundamental property that arises from the random nature of its movements. This property has important implications in various applications of Brownian motion, such as option pricing in finance and modeling diffusion processes in physics.

Understanding Brownian Motion

Brownian motion is a stochastic process that describes the random movement of particles in a fluid or gas. It was first observed by the botanist Robert Brown in 1827, while studying pollen grains suspended in water. The motion of these particles appeared to be erratic and unpredictable.

Later, Albert Einstein provided a theoretical explanation for this phenomenon in 1905, which is now known as the Einstein-Smoluchowski equation. According to this equation, the motion of particles in a fluid is due to the collisions with the surrounding molecules. These collisions cause the particles to move randomly in different directions.

The expectation of Brownian motion refers to the average value of the motion over time. In the case of Brownian motion, the expectation is defined as the average position of the particle at any given time. However, why is the expectation of Brownian motion 0?

The reason for this is that Brownian motion is a symmetric process. This means that the particles have an equal chance of moving in any direction. As a result, the positive and negative displacements cancel each other out over a large number of steps.

To understand this concept, consider a particle initially at the origin (0,0) in a two-dimensional space. As the particle moves, it can take steps in any direction randomly. Each step has an equal probability of being positive or negative, resulting in a symmetric distribution of displacements.

Step	Displacement
1	+1
2	-2
3	+3
4	-4
5	-1

As seen in the table above, the displacements are random and can either be positive or negative. However, when we take the average of these displacements over a large number of steps, we observe that the positive and negative values cancel each other out, resulting in an average displacement of zero.

Mathematically, we can express the expectation of Brownian motion as E[X(t)] = 0, where X(t) denotes the position of the particle at time t. This property holds for both one-dimensional and multi-dimensional Brownian motion.

Read Also: What Does MMR Stand For? Get the Meaning and Definition

Understanding the expectation of Brownian motion is crucial in various fields, including finance, physics, and biology. It allows us to make predictions and analyze the behavior of particles in a wide range of applications.

Theoretical Background

In order to understand why the expectation of Brownian motion is 0, it is necessary to delve into the theoretical background of the concept.

Read Also: Understanding the Difference between PACF and ACF: Key Concepts Explained

Brownian motion, named after the botanist Robert Brown who first observed this phenomenon in 1827, refers to the random motion of particles in a fluid. It is widely used in various fields such as physics, finance, and biology to model random processes.

The mathematical model of Brownian motion, also known as a Wiener process, was introduced by the mathematician Norbert Wiener in 1923. It is characterized by two main properties: randomness and continuity.

One of the fundamental properties of Brownian motion is that it has stationary and independent increments. This means that the increments of the process over non-overlapping intervals are independent of each other and their distribution does not depend on the starting point of the interval.

Another key property of Brownian motion is that it is a martingale. A martingale is a stochastic process in which the expected value of the next observation, given the current one, is equal to the current value. This property holds for Brownian motion, which makes it a fundamental concept in probability theory.

Now, let’s consider the expectation of Brownian motion. The expectation, also known as the average or mean, is a measure of the central tendency of a random variable. For a continuous random variable like Brownian motion, the expectation can be interpreted as the geometric center of its distribution.

Since Brownian motion is a martingale, its expectation at any given time t, denoted by E[W(t)], is equal to its initial value at time 0. In other words, the expectation of Brownian motion is 0, assuming it starts at the origin.

This result can be explained by the symmetric nature of Brownian motion. The process exhibits equal probabilities of moving up or down, resulting in a net average of 0. The randomness and continuity of Brownian motion ensure that its trajectory is equally likely to move in any direction, which leads to an expectation of 0.

In conclusion, the expectation of Brownian motion is 0 due to its martingale property and the symmetric nature of its movements. Understanding this theoretical background is crucial in applications of Brownian motion and in various fields that rely on random processes.

FAQ:

What is Brownian motion?

Brownian motion is a random motion of particles suspended in a fluid, caused by the random collisions with molecules of the fluid. It was first observed by the botanist Robert Brown in 1827.

Why is the expectation of Brownian motion 0?

The expectation of Brownian motion is 0 because it is a random walk with equal probability of moving in any direction. Therefore, on average, it does not move in any particular direction over time.

Is Brownian motion always centered at 0?

Yes, Brownian motion is always centered at 0 in the long run. Although it can move away from the origin in the short term, over time it tends to return to and stay around the origin due to its inherent randomness.

What does it mean for the expectation of Brownian motion to be 0?

When the expectation of Brownian motion is 0, it means that, on average, the motion does not have a systematic drift or trend over time. It is equally likely to move in positive or negative directions, balancing out any overall movement.