What is a residual in MA model? Understanding the concept of residuals in moving average models

What is a residual in MA model?

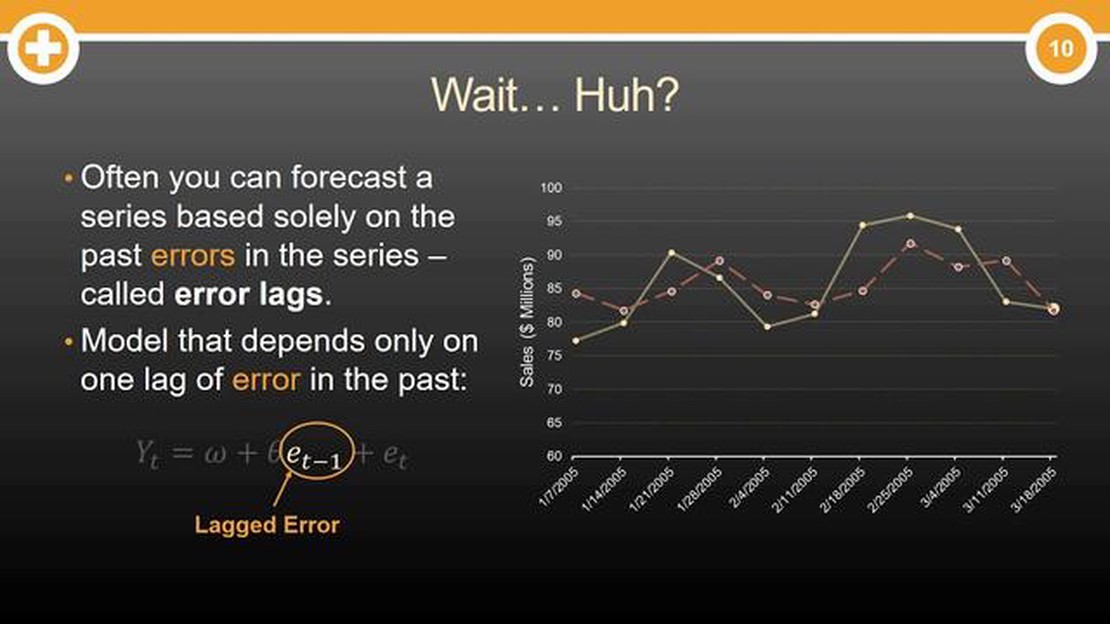
In time series analysis, a moving average (MA) model is a commonly used method to forecast future values based on past observations. It helps to identify underlying trends and patterns in the data. A key component of the MA model is the residual, which plays a crucial role in determining the accuracy of the model.

The residual, also known as the error term, is the difference between the observed value and the predicted value from an MA model. It represents the part of the data that cannot be explained by the model. In other words, it captures the random variation or noise in the data that is not accounted for by the model.

Table Of Contents

For example, let’s say we have a sales dataset and we want to use an MA model to forecast future sales. The model estimates the expected sales based on the past observations. The residual is then calculated by subtracting the predicted sales from the actual sales. It tells us how well the model is able to capture the true sales pattern.

The residuals in an MA model are typically assumed to be normally distributed with mean zero and constant variance. This assumption is essential for the model to make accurate predictions. If the residuals do not follow a normal distribution or exhibit a pattern, it indicates that the model may not be capturing all the relevant information in the data.

An important task in MA modeling is to analyze the residuals and check for any patterns or outliers. This can be done using statistical tests or visual examination of residual plots. By understanding the properties of the residuals, we can assess the adequacy of the MA model and make necessary adjustments to improve its performance.

What is a residual in MA model?

In the context of moving average (MA) models, a residual refers to the difference between the observed values and the predicted values at each point in the time series. It represents the unexplained portion of the data that cannot be accounted for by the model.

The MA model is a type of time series model that represents the observed values as a function of the past error terms and current random shocks. These error terms are also known as residuals. In an MA model, the residuals are assumed to be white noise, which means that they are uncorrelated and have constant variance.

When fitting an MA model to a time series, the parameters of the model are estimated using a statistical technique called maximum likelihood estimation. Once the model is fitted, the residuals are calculated by subtracting the predicted values from the observed values. The residuals can be used to assess the goodness of fit of the model, test for the presence of autocorrelation, and identify outliers or unusual patterns in the data.

By examining the residuals, analysts can determine whether the model adequately captures the underlying patterns and dynamics of the time series. If the residuals exhibit autocorrelation or have non-constant variance, it suggests that the model is misspecified and needs to be revised. Conversely, if the residuals show no evidence of autocorrelation and have constant variance, it indicates that the model is a good approximation of the data.

Read Also: Discover the Average Exchange Rate in Singapore | Expert Guide

Example

Suppose we have a time series of monthly sales data for a particular product. We want to model the sales using an MA(1) model, which means that the observed values are a function of the current error term and the error term from the previous month. After estimating the parameters of the model, we calculate the residuals by subtracting the predicted sales from the observed sales for each month. By analyzing the residuals, we can determine if the MA(1) model adequately explains the variation in the sales data.

Month	Observed Sales	Predicted Sales	Residual
January	100	90	10
February	95	105	-10
March	110	100	10
April	105	110	-5
May	120	115	5

In this example, the residuals indicate the deviations between the observed sales and the predicted sales based on the MA(1) model. The positive and negative residuals suggest that the model slightly underestimates the sales in January and April, respectively. By examining the patterns in the residuals, we can make further adjustments to the model to improve its accuracy in predicting future sales.

Understanding the concept of residuals in moving average models

In a moving average (MA) model, residuals play a crucial role in understanding the model’s performance and validity. Residuals represent the difference between the observed value and the predicted value from the MA model.

When fitting an MA model to a dataset, the model makes predictions based on a linear combination of past observed values and current error terms. The residuals are calculated as the difference between the observed values and the predicted values. They provide an indication of how well the MA model fits the data.

The residuals in an MA model should ideally have the following properties:

Read Also: The MUI's Fatwa: Understanding the Regulation of Buying and Selling Al Sharf Currency

Zero mean: The residuals should have a mean of zero. If the mean is significantly different from zero, it suggests that the model is not able to capture the underlying pattern in the data.
Constant variance: The residuals should have constant variance. If the variance of the residuals is not constant, it indicates the presence of heteroscedasticity, which implies that the model’s assumptions are violated.
Independence: The residuals should be independent and not exhibit any temporal dependencies or correlations. If there is a correlation between the residuals, it suggests that the model is not accounting for all the information present in the data.

To assess the properties of the residuals, various diagnostic tests and visualizations can be used. Some commonly used diagnostic techniques include:

Ljung-Box test: This test checks for autocorrelation in the residuals.
Q-Q plot: This plot compares the distribution of the residuals against a theoretical normal distribution.
Residual plot: This plot shows the residuals over time and helps identify any patterns or trends.
Autocorrelation plot: This plot displays the autocorrelation of the residuals at different lags.

By analyzing the residuals and using these diagnostic tools, it is possible to identify any issues with the MA model and make necessary adjustments. Understanding and monitoring the concept of residuals is essential to ensure accurate and reliable predictions from the MA model.

FAQ:

What are residuals in a moving average model?

Residuals in a moving average (MA) model represent the difference between the observed values and the predicted values. They are the unexplained part of the data that cannot be accounted for by the model.

How are residuals calculated in a moving average model?

Residuals in a moving average (MA) model are calculated by subtracting the predicted values from the observed values. The difference between the observed and predicted values gives us the residual for each data point.

What do positive residuals mean in a moving average model?

Positive residuals in a moving average (MA) model indicate that the observed values are higher than the predicted values. This suggests that the model has underestimated the values or there may be some other factors influencing the data that are not captured by the model.

Are residuals in a moving average model always normally distributed?

In theory, residuals in a moving average (MA) model should follow a normal distribution. However, in practice, this may not always be the case. Residuals can deviate from normality due to various reasons such as outliers, misspecification of the model, or violation of assumptions.

What can we learn from analyzing residuals in a moving average model?

Analyzing residuals in a moving average (MA) model can provide insights into the adequacy of the model. By examining the patterns and properties of residuals, we can assess whether the model captures all the important information in the data or if there are underlying trends, seasonality, or other factors that need to be included in the model.

What is a moving average model?

A moving average (MA) model is a statistical model commonly used in time series analysis to forecast future values of a variable based on its past values. It is a type of linear model that incorporates a moving average of the past error terms.