Understanding the Impulse Response of the Moving Average System

Impulse response of the moving average system

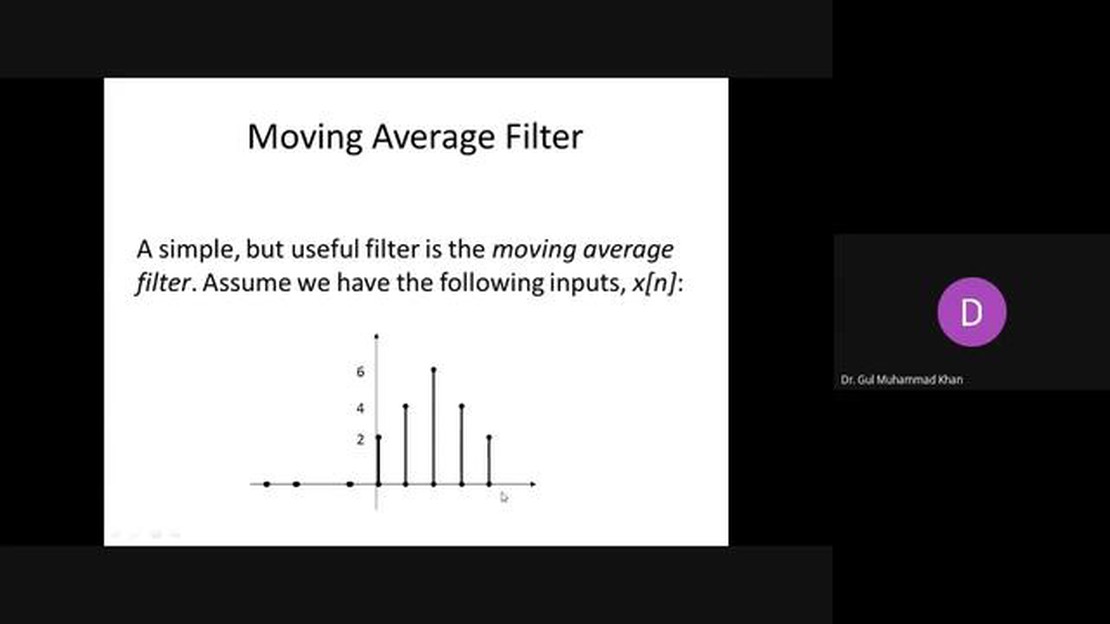
When it comes to analyzing and understanding signals in various fields, the impulse response of a system is a key concept. In the field of signal processing, the moving average system is a commonly used system for analyzing time series data. The impulse response of this system provides valuable insight into how the system behaves and responds to different inputs.

The moving average system is a filter that calculates the average value of a specified number of consecutive data points. It is often used to smooth out noisy data or to identify underlying trends in a time series. By understanding the impulse response of this system, we can gain a deeper understanding of its behavior and its impact on the signals being analyzed.

Table Of Contents

The impulse response of the moving average system represents the output of the system when an impulse, or a single sample with an amplitude of 1, is applied to the input. This impulse acts as a test signal, allowing us to observe how the system responds and how it affects subsequent data points. By studying the impulse response, we can determine important characteristics of the system, such as its linearity, time shift, and frequency response.

By analyzing the impulse response of the moving average system, we can gain insights into how it affects the signals being processed. For example, we can examine the system’s ability to suppress high-frequency noise or its impact on the amplitude and phase of different frequency components. This knowledge is crucial for understanding the limitations and capabilities of the moving average system and for making informed decisions about its application in different fields.

What is the Impulse Response?

The impulse response is a concept in signal processing that helps to understand how a system responds to an input signal. It can be defined as the output of a system when an impulse signal, also known as a Dirac delta function, is applied as the input.

An impulse signal is a very short duration signal with an area of one unit, where it is zero everywhere except at a single point where it is infinite. The impulse response is obtained by convolving the impulse signal with the system’s transfer function.

The impulse response provides important information about the system’s characteristics and behavior. It represents the system’s output for different time instants after the input impulse is applied. By analyzing the impulse response, one can determine the system’s stability, linearity, and time-invariance.

The impulse response is also used to obtain the frequency response of a system. The frequency response represents how a system attenuates or amplifies different frequency components of a signal. It can be obtained by taking the Fourier transform of the impulse response.

In summary, the impulse response is a valuable tool in signal processing that allows us to understand how a system reacts to an input signal, and provides insight into its behavior and characteristics.

Properties of the Impulse Response

The impulse response of a system provides valuable information about its characteristics and behavior. Several properties can be derived from the impulse response.

1. Linearity: If a system is linear, its impulse response can be expressed as the weighted sum of scaled and shifted versions of the input impulsive signal. This property allows for the superposition of input signals.

2. Time-Invariance: A system is time-invariant if the impulse response is constant over time. This means that the behavior of the system remains the same regardless of when the input impulse is applied.

3. Causality: A causal system is one in which the impulse response is nonzero only for nonnegative time values. This implies that the output of the system at any given time depends only on the current and past values of the input signal.

Read Also: What is the 9 20 intraday strategy? A guide to effective intraday trading

4. Stability: Stability of a system can be determined from its impulse response. A system is stable if the absolute sum of the impulse response is finite. This ensures that the system’s output remains bounded for any bounded input.

5. Frequency Response: The frequency response of a system can be obtained from its impulse response using the Fourier transform. It provides information about the system’s behavior in the frequency domain.

6. Convolution: Convolution is a mathematical operation used to describe the output of a system given an input signal and the impulse response. The impulse response is convolved with the input signal to obtain the system’s output.

These properties are fundamental in understanding and analyzing the behavior of systems using the impulse response. They allow engineers and researchers to predict and control the response of the system to different input signals.

Moving Average System and its Impulse Response

A moving average system is a commonly used filter in signal processing and time series analysis. It is a linear time-invariant system that processes a given input by taking the average of a fixed number of past input samples. This average is then used as the output of the system at each time step.

The impulse response of a moving average system represents the system’s output when an impulse signal is inputted. An impulse signal is a signal that is zero everywhere except at time zero, where it is equal to one. By applying an impulse signal to the input of a moving average system, we can determine the system’s response and better understand its characteristics.

The impulse response of a moving average system can be expressed mathematically as a sequence of weights, where each weight corresponds to the amplitude of the system’s output at a particular time lag. These weights are equal to the reciprocal of the number of past input samples that are included in the moving average calculation.

To visualize the impulse response of a moving average system, it is common to use a table. The table consists of two columns: the time lag (t) and the weight (w). The time lag represents the number of time steps between the current output and the corresponding input sample. The weight represents the amplitude of the system’s output at that particular time lag.

Read Also: Understanding the Concept of .01 Lot Size in Forex and Its Significance

For example, let’s consider a moving average system that takes the average of the current and previous two input samples. The impulse response of this system can be represented as follows:

Time Lag (t)	Weight (w)
0	0.5
1	0.25
2	0.25

In this example, at time lag 0, the weight is 0.5, indicating that the system’s output is half of the input sample at that time step. At time lag 1 and 2, the weights are 0.25, indicating that the system’s output is a quarter of the corresponding input samples.

Understanding the impulse response of a moving average system is crucial for analyzing its filtering properties and its effect on different types of input signals. By studying the impulse response, we can gain insights into how the system attenuates or amplifies certain frequency components and how it affects the overall signal quality.

In conclusion, the moving average system is a widely used filter in signal processing, and its impulse response provides valuable information about its behavior and characteristics. The impulse response can be visualized using a table to show the weights at different time lags, allowing for a better understanding of the system’s filtering properties.

FAQ:

What is the impulse response of a moving average system?

The impulse response of a moving average system is the output of the system when an impulse input is applied to it.

How can the impulse response of a moving average system be calculated?

The impulse response of a moving average system can be calculated by taking the average of the input samples within a certain window of time.

What can the impulse response of a moving average system tell us about the system?

The impulse response of a moving average system can tell us about the system’s ability to smooth out or filter input signals. It can also provide insights into the system’s frequency response and stability.

Is the impulse response of a moving average system always finite?

Yes, the impulse response of a moving average system is always finite because it is only computed over a finite window of time. This is in contrast to other systems, such as infinite impulse response (IIR) filters, which may have infinite impulse responses.

Can we determine the impulse response of a moving average system by analyzing its transfer function?

Yes, the impulse response of a moving average system can be determined by analyzing its transfer function. The transfer function of a moving average system is the z-transform of its impulse response.