Understanding the Distinctions between AR1 and AR2 Model

What is the Difference Between AR1 and AR2 Models?

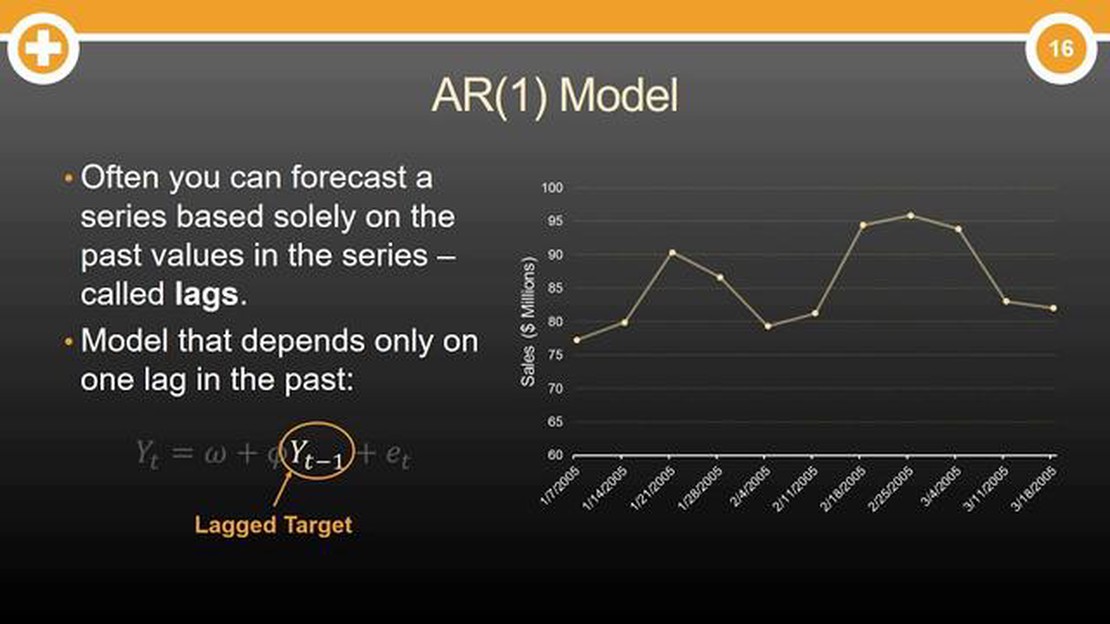
Autoregressive models (AR models) are an essential tool in time series analysis and forecasting. These models describe how a given variable is related to its past values. Two commonly used AR models are the AR1 and AR2 models. While both models involve the relationship between a variable and its lagged values, there are distinct differences between them that are crucial to understand.

Table Of Contents

The AR1 model assumes that the current value of a variable is only dependent on its immediate past value. In other words, it considers only the lag-1 term in the autoregressive equation. This model is also known as a first-order autoregressive model. It is characterized by a single coefficient that captures the relationship between the current value and the lag-1 value.

On the other hand, the AR2 model takes into account the current and the immediate past value of a variable. It considers the lag-1 and lag-2 terms in the autoregressive equation. This model is also known as a second-order autoregressive model. It is characterized by two coefficients, each corresponding to the lag-1 and lag-2 values, respectively.

Understanding the distinctions between the AR1 and AR2 models is crucial in time series analysis, as it impacts the accuracy of forecasts and the insights gained from analyzing the data. Both models have their strengths and limitations, and the choice between them depends on the specific characteristics of the dataset and the goals of the analysis. By understanding these distinctions, analysts can make informed decisions about which model to use, leading to more accurate and meaningful results.

A Brief Overview of AR Models

An Autoregressive (AR) model is a type of time series model that is used to describe and forecast future values based on previous observations. It is commonly used in econometrics, finance, and other fields where the data has a temporal arrangement.

The AR model is based on the assumption that the current value of a variable is a linear combination of its past values and a random error term. The model can be represented as:

AR(1) Model	AR(2) Model
Y(t) = α + φ₁Y(t-1) + ε(t)	Y(t) = α + φ₁Y(t-1) + φ₂Y(t-2) + ε(t)

In the AR(1) model, the variable Y at time t is a function of its previous value Y(t-1) and an error term ε(t). The parameter φ₁ represents the autoregressive coefficient, which reflects the influence of the previous value on the current value.

The AR(2) model builds upon the AR(1) model by including an additional lagged term. In this case, the variable Y at time t also depends on its value two time periods ago, Y(t-2). The autoregressive coefficients φ₁ and φ₂ determine the influence of the lagged values on the current value.

AR models are useful for analyzing and forecasting time series data. They can capture patterns and trends in the data, and provide insights into the relationship between past and future values. The choice between AR(1) and AR(2) depends on the specific dataset and the complexity of the underlying process being modeled.

Understanding AR1 Model

The AR1 model, also known as the autoregressive model of order 1, is a time series model that represents the value of a variable at a given time as a linear combination of its past values and a random error term.

In the AR1 model, the value of the variable at time t is dependent on its value at time t-1, with the assumption that the impact of previous values on the current value decreases over time. This means that the variable has a memory of its past values, but the importance of these values diminishes as we move further away from the current time point.

The AR1 model can be expressed as:

Yt = c + φ1Yt-1 + εt

Where:

Read Also: What time does the Japanese forex market open?

Yt represents the value of the variable at time t
c is a constant term
φ1 is the autoregressive coefficient, which determines the impact of the previous value on the current value
εt is a random error term with zero mean and constant variance

The AR1 model is widely used in time series analysis as it captures the persistent dependence between consecutive observations. It allows for forecasting future values based on past observations and can be used to identify patterns, trends, and seasonality in the data.

It is important to note that the AR1 model assumes stationarity of the time series, which means that the mean, variance, and autocovariance are constant over time. If the time series is non-stationary, it may be necessary to apply transformations or differencing to make it stationary before fitting an AR1 model.

Understanding AR2 Model

In time series analysis, an autoregressive model of order 2, commonly referred to as AR2 model, is a mathematical representation of a time series that incorporates the relationship between current and past observations up to two lags. The AR2 model is an extension of the AR1 model and provides a more sophisticated description of the underlying temporal dynamics.

Similar to the AR1 model, the AR2 model assumes that the current observation in a time series is a linear combination of the past two observations, plus an error term. Mathematically, the equation for the AR2 model is represented as:

Read Also: Best Platforms for Trading Option Spreads - Find the Perfect Option Spread Trading Platform


yt = α + β1 * yt-1 + β2 * yt-2 + et

where yt represents the current observation, yt-1 and yt-2 represent the observations at lag 1 and lag 2 respectively, α is the intercept term, β1 and β2 are the coefficients that represent the strength of the relationship between the current observation and the past observations, and et is the error term.

The AR2 model allows for capturing more complex temporal patterns and dependencies compared to the AR1 model. By incorporating past two observations, it can account for trends and patterns that may span over two time points. This additional flexibility can lead to improved forecasting accuracy and a better understanding of the underlying data generating process.

However, it is important to note that as the order of the autoregressive model increases, the number of parameters to estimate also increases. This can lead to increased computational complexity and the need for larger data sets for reliable parameter estimation.

In summary, the AR2 model is a valuable tool in time series analysis as it considers the relationship between the current observation and the two previous observations. By incorporating more historical information, the AR2 model provides a more nuanced understanding of the underlying temporal dynamics, allowing for improved forecasting and analysis of time series data.

FAQ:

What are the main differences between AR1 and AR2 models?

The main difference between AR1 and AR2 models is the number of lagged values that are included in the model. AR1 model uses only one lagged value, while AR2 model uses two lagged values.

Why would someone choose to use an AR1 model over an AR2 model?

One possible reason to choose an AR1 model over an AR2 model is if the additional lagged values do not significantly improve the model’s performance or if the coefficients for the additional lagged values are not statistically significant.

Are AR1 and AR2 models suitable for all types of data?

AR1 and AR2 models are commonly used for time series data, where the observations are recorded at regular intervals over time. However, the suitability of these models depends on the specific characteristics and patterns present in the data.

How can one determine the appropriate lag order for an autoregressive model?

There are several methods for determining the appropriate lag order for an autoregressive model, such as the Akaike Information Criterion (AIC) and the Bayesian Information Criterion (BIC). These criteria aim to find a balance between model complexity and goodness of fit.

Can AR1 and AR2 models capture nonlinear patterns in the data?

No, AR1 and AR2 models are linear models that assume a linear relationship between the lagged values and the current value. If the data exhibits nonlinear patterns, more sophisticated models, such as ARIMA or GARCH, may be more appropriate.

What is the difference between an AR1 model and an AR2 model?

An AR1 model is a first-order autoregressive model that predicts a future value based on a single past value. An AR2 model is a second-order autoregressive model that considers two past values to predict a future value.

How is the AR1 model different from the AR2 model?

The main difference between the AR1 model and the AR2 model is the number of past values considered to predict a future value. The AR1 model only considers one past value, while the AR2 model considers two past values.