Is Black-Scholes a binomial model? Exploring the relationship between the Black-Scholes pricing model and binomial models

Comparing the Black-Scholes Model and the Binomial Model

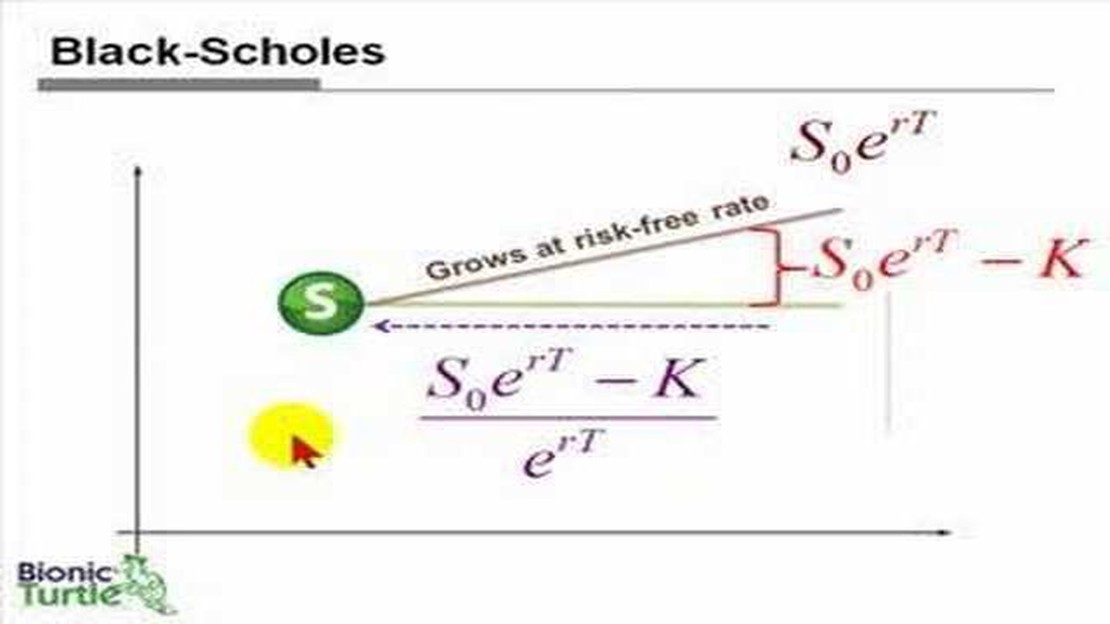
The Black-Scholes pricing model is widely used in the field of finance for estimating the price of financial derivatives, such as options contracts. However, there is an ongoing debate regarding whether Black-Scholes can be considered a binomial model. In this article, we will delve into the relationship between the Black-Scholes model and binomial models, and examine the similarities and differences between the two.

First, let’s define what a binomial model is. A binomial model is a mathematical model that represents the possible outcomes of an event with two possible values, typically referred to as “up” and “down.” This type of model is often used to price options by considering the possible price movements of the underlying asset over a series of discrete time steps.

Table Of Contents

The Black-Scholes model, on the other hand, is a continuous-time model that assumes the price of the underlying asset follows a geometric Brownian motion. It takes into account factors such as time, volatility, risk-free interest rate, and strike price to estimate the value of an option. The continuous nature of the Black-Scholes model sets it apart from binomial models, which consider discrete time steps.

While the Black-Scholes model is not strictly a binomial model, it can be viewed as a limiting case of a binomial model as the number of time steps approaches infinity. In other words, as the number of time steps increases, the binomial model converges to the Black-Scholes model. This is known as the convergence principle, which states that binomial models converge to continuous-time models under certain assumptions.

Is Black-Scholes a binomial model?

The Black-Scholes pricing model is a widely used mathematical model for pricing options, which takes into account various factors such as the current price of the underlying asset, the time until expiration, the volatility of the asset, and the risk-free interest rate. It was developed by economists Fischer Black and Myron Scholes in the early 1970s.

While the Black-Scholes model is not a binomial model in its original form, there is a close relationship between the two. The Black-Scholes model assumes a continuous distribution of the underlying asset’s price, whereas binomial models, such as the Cox-Ross-Rubinstein model, assume a discrete distribution of prices. However, as the time periods in a binomial model become infinitesimally small, the model approaches a continuous distribution and converges towards the Black-Scholes model.

In fact, the Black-Scholes model can be derived from the binomial model through a process known as the “binomial approximation.” This involves taking the limit of the binomial model as the number of time periods approaches infinity and the time between each period becomes infinitesimally small. The resulting equation is the continuous Black-Scholes equation.

However, it is important to note that the binomial model and the Black-Scholes model have different assumptions and limitations. The binomial model is more flexible and can handle situations where the underlying asset’s price is subject to jumps or other discontinuous movements. On the other hand, the Black-Scholes model assumes constant volatility and a continuous price distribution, which may not always accurately reflect market conditions.

Overall, while the Black-Scholes model is not a binomial model in its original form, it can be derived from the binomial model through an approximation process. The two models have a close relationship, but also have differences in their assumptions and limitations.

Understanding the Black-Scholes pricing model and its relationship with binomial models

The Black-Scholes pricing model is a mathematical model used to calculate the theoretical price of options. It was developed by economists Fisher Black and Myron Scholes in 1973 and has become the standard model for option pricing in financial markets.

Read Also: What Does SMA Say? Insights and Analysis

The model is based on several assumptions, including the assumption that the price of the underlying asset follows a geometric Brownian motion. This assumption allows for the calculation of the probability distribution of the future price of the asset, which is a key component in determining option prices.

The Black-Scholes model is a continuous-time model, meaning it assumes that the price movements of the underlying asset are continuous and can be modeled using differential equations. However, in practice, many assets have discrete price movements, which can make the Black-Scholes model less accurate.

Read Also: Step-by-step guide: How to get foreign currency from Absa

This is where binomial models come into play. Binomial models are discrete-time models that divide the time period into a number of smaller intervals and assume that the price of the underlying asset can either go up or down during each interval. By constructing a binomial tree of possible asset prices, it is possible to determine the value of an option at each node of the tree and then work backward to calculate the option’s present value.

The relationship between the Black-Scholes model and binomial models is that binomial models can be seen as approximations of the continuous-time Black-Scholes model. As the number of intervals in the binomial model increases, the model becomes more accurate and approaches the results obtained from the continuous-time Black-Scholes model.

However, it is important to note that the binomial model requires more computational effort and can be more time-consuming compared to the Black-Scholes model. This is because the binomial model calculates the option value at each node in the tree, whereas the Black-Scholes model provides a closed-form equation that can be solved directly.

In conclusion, the Black-Scholes pricing model and binomial models are both used to calculate option prices, but they differ in their assumptions and approach. While the Black-Scholes model is based on continuous-time and continuous-price movements, binomial models are based on discrete-time and discrete-price movements. Binomial models can be considered as approximations of the Black-Scholes model and provide a more accurate estimate of option prices when the underlying asset has discrete price movements.

FAQ:

What is the Black-Scholes pricing model?

The Black-Scholes pricing model is a mathematical model used to calculate the theoretical price of options. It takes into consideration factors such as the current stock price, the strike price of the option, the time until expiration, and the volatility of the underlying stock.

How does the Black-Scholes pricing model work?

The Black-Scholes pricing model uses a set of equations to calculate the fair value of an option. It assumes that the price of the underlying stock follows a geometric Brownian motion, and it takes into account the risk-free interest rate and the time until expiration. By inputting these variables into the model, it provides an estimate of the option’s value.

What are binomial models in options pricing?

Binomial models are a type of mathematical model used in options pricing. They are based on the assumption that the price of the underlying stock can only move up or down by a certain amount during each time period. By calculating the possible price movements and probabilities of those movements, binomial models can estimate the value of an option.

Is the Black-Scholes pricing model a binomial model?

No, the Black-Scholes pricing model is not a binomial model. It is a continuous model that assumes the price of the underlying stock follows a geometric Brownian motion. In contrast, binomial models consider a discrete set of possible price movements and their probabilities.

What are some advantages of using the Black-Scholes pricing model over binomial models?

One advantage of the Black-Scholes pricing model is that it is a more efficient and faster method for calculating option prices compared to binomial models. It also provides a more accurate estimate of the fair value of options for European-style options, where the exercise can only occur at expiration. Binomial models, on the other hand, can be more computationally intensive and are better suited for pricing American-style options with early exercise opportunities.